OpenStax University Physics/V1/Equations

Template:EduV/announcement Equations lifted from chapter summaries in https://cnx.org/contents/1Q9uMg_a@9.7:Gofkr9Oy@10/Preface

Do not edit this page. Instead copy and paste the source wikitext somewhere else. See these two examples:
WSU Lake University Physics V1 equations
Formulas (in compact form)
Volume 2 equations are complete

Introduction

metric prefixes

da	h	k	M	G	T	P	E	Z	Y
deca	hecto	kilo	mega	giga	tera	peta	exa	zetta	yotta
1E+01	1E+02	1E+03	1E+06	1E+09	1E+12	1E+15	1E+18	1E+21	1E+24
d	c	m	µ	n	p	f	a	z	y
deci	centi	milli	micro	nano	pico	femto	atto	zepto	yocto
1E-01	1E-02	1E-03	1E-06	1E-09	1E-12	1E-15	1E-18	1E-21	1E-24

Units_and_Measurement

The base SI units are mass: kg (kilogram); length: m (meter); time: s (second). Percent error is $(\delta A/A)\times 100\%$

Vectors

Vector ${\vec {A}}=A_{x}\,{\hat {i}}+A_{y}\,{\hat {j}}+A_{z}\,{\hat {k}}$ involves components (A_x,A_y,A_z) and three orthonormal unit vectors.

▭ If ${\vec {A}}+{\vec {B}}={\vec {C}}$, then A_x+B_x=C_x, etc, and vector subtraction is defined by ${\vec {B}}={\vec {C}}-{\vec {A}}$.

▭ The two-dimensional displacement from the origin is ${\vec {r}}=x{\hat {i}}+y{\hat {j}}$. The magnitude is $A\equiv |{\vec {A}}|={\sqrt {A_{x}^{2}+A_{y}^{2}}}$. The angle (phase) is $\theta =\tan ^{-1}{(y/x)}$.

▭ Scalar multiplication $\alpha {\vec {A}}=\alpha A_{x}{\hat {i}}+\alpha A_{y}{\hat {j}}+...\quad$

▭ Any vector divided by its magnitude is a unit vector and has unit magnitude: $|{\hat {V}}|=1$ where ${\hat {V}}\equiv {\vec {V}}/V$

▭ Dot product ${\vec {A}}\cdot {\vec {B}}=AB\cos \theta =A_{x}B_{x}+A_{y}B_{y}+...\quad$ and ${\vec {A}}\cdot {\vec {A}}=A^{2}$

▭ Cross product ${\vec {A}}={\vec {B}}\times {\vec {C}}\Rightarrow$ $A_{\alpha }=B_{\beta }C_{\gamma }-C_{\gamma }A_{\beta }$ where $(\alpha ,\beta ,\gamma )$ is any cyclic permutation of $(x,y,z)$, i.e., (α,β,γ) represents either (x,y,z) or (y,z,x) or (z,x,y).

▭ Cross-product magnitudes obey $A=BC\sin \theta$ where $\theta$ is the angle between ${\vec {B}}$ and ${\vec {C}}$, and ${\vec {A}}\perp \{{\vec {B}},{\vec {C}}\}$ by the right hand rule.

▭ Vector identities $\;c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B} \quad$

▭ $\mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A} \quad$

▭ $\mathbf {A} +(\mathbf {B} +\mathbf {C} )=(\mathbf {A} +\mathbf {B} )+\mathbf {C} \quad$

▭ $\mathbf {A} \cdot \mathbf {B} =\mathbf {B} \cdot \mathbf {A} \quad$

▭ $\mathbf {A} \times \mathbf {B} =\mathbf {-B} \times \mathbf {A} \quad$

▭ $\left(\mathbf {A} +\mathbf {B} \right)\cdot \mathbf {C} =\mathbf {A} \cdot \mathbf {C} +\mathbf {B} \cdot \mathbf {C} \quad$

▭ $\left(\mathbf {A} +\mathbf {B} \right)\times \mathbf {C} =\mathbf {A} \times \mathbf {C} +\mathbf {B} \times \mathbf {C} \quad$

▭ $\mathbf {A} \cdot \left(\mathbf {B} \times \mathbf {C} \right)=\mathbf {B} \cdot \left(\mathbf {C} \times \mathbf {A} \right)=\left(\mathbf {A} \times \mathbf {B} \right)\cdot \mathbf {C} \quad$

▭ $\mathbf {A\times } \left(\mathbf {B} \times \mathbf {C} \right)=\left(\mathbf {A} \cdot \mathbf {C} \right)\mathbf {B} -\left(\mathbf {A} \cdot \mathbf {B} \right)\mathbf {C} \quad$

▭ $\mathbf {\left(A\times B\right)\cdot } \left(\mathbf {C} \times \mathbf {D} \right)=\left(\mathbf {A} \cdot \mathbf {C} \right)\left(\mathbf {B} \cdot \mathbf {D} \right)-\left(\mathbf {B} \cdot \mathbf {C} \right)\left(\mathbf {A} \cdot \mathbf {D} \right)$

Motion_Along_a_Straight_Line

Delta as difference $\Delta x=x_{f}-x_{i}\rightarrow dx\rightarrow 0$ in limit of differential calculus.

▭ Average velocity ${\bar {v}}=\Delta x/\Delta t\rightarrow v=dx/dt$ (instantaneous velocity)

▭ Acceleration ${\bar {a}}=\Delta v/\Delta t\rightarrow a=dv/dt$.

▭ WLOG set $\Delta t=t\;$ and $\Delta x=x-x_{0}\;$ if $t_{i}=0$. Then $\Delta v=v-v_{0}$, and $\;v(t)=\int _{0}^{t}a(t')dt'+v_{0}$, $\;x(t)=\int _{0}^{t}v(t')dt'+x_{0}=x_{0}+{\bar {v}}t$, where ${\bar {v}}={\frac {1}{t}}\int _{0}^{t}v(t')dt'$ is the average velocity.

▭ At constant acceleration: ${\bar {v}}={\tfrac {v_{0}+v}{2}},\quad v=v_{0}+at,\quad x=x_{0}+v_{0}t+{\tfrac {1}{2}}at^{2},\,$ $v^{2}=v_{0}^{2}+2a\Delta x$.

▭ For free fall, replace $x\rightarrow y$ (positive up) and $a\rightarrow -g$, where $g$ = 9.81 m/s² at Earth's surface).

Motion_in_Two_and_Three_Dimensions

Instantaneous velocity: ${\vec {v}}(t)=v_{x}(t){\hat {i}}+v_{y}(t){\hat {j}}+v_{z}(t){\hat {k}}\;={\frac {dx}{dt}}{\hat {i}}+{\frac {dy}{dt}}{\hat {j}}+{\frac {dz}{dt}}{\hat {k}}\;$ $=\lim _{\Delta t\rightarrow 0}{\tfrac {\Delta {\vec {r}}}{\Delta t}}=\lim _{\Delta t\rightarrow 0}{\tfrac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}$, where ${\vec {r}}(t)=x(t){\hat {i}}+y(t){\hat {j}}+z(t){\hat {k}}$

▭ Acceleration ${\vec {a}}=a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}}$, where $a_{x}(t)=dv_{x}/dt=d^{2}x/dt^{2}$.

▭ Average values: ${\vec {v}}_{ave}={\tfrac {\Delta {\vec {r}}}{\Delta t}}={\tfrac {{\vec {r}}(t_{2})-{\vec {r}}(t_{2})}{t_{2}-t_{1}}}$, and $\;{\vec {a}}_{ave}={\tfrac {\Delta {\vec {v}}}{\Delta t}}={\tfrac {{\vec {v}}(t_{2})-{\vec {v}}(t_{2})}{t_{2}-t_{1}}}$

▭ Free fall time of flight $\,T_{of}={\tfrac {2(v_{0}\sin \theta _{0})}{g}}\,,\,$ ▭ Trajectory $y=(\tan \theta _{0})x-\left[{\tfrac {g}{2(v_{0}\cos \theta _{0})^{2}}}\right]x^{2}\,,\,$ ▭ Range $R={\tfrac {v_{0}^{2}\sin 2\theta _{0}}{g}}$

▭ Uniform circular motion: $|{\vec {a}}|=a_{C}=\omega ^{2}r=v^{2}/r$ where $v\equiv |{\vec {v}}|=\omega r$

${\vec {r}}=A\cos \omega t{\hat {i}}+A\sin \omega t{\hat {j}}\,,\,$ ${\vec {v}}=-A\omega \sin \omega t{\hat {i}}+A\omega \cos \omega t{\hat {j}}\,,\,$ ${\vec {a}}=-A\omega ^{2}\cos \omega t{\hat {i}}-A\omega ^{2}\sin \omega t{\hat {j}}\,.$

▭ Tangential and centripetal acceleration ${\vec {a}}={\vec {a}}_{c}+{\vec {a}}_{T}$ where $a_{T}=d|{\vec {v}}|/dt$.

▭ Relative motion: $\,{\vec {r}}_{PS}={\vec {r}}_{PS'}+{\vec {r}}_{S'S}$, $\,{\vec {v}}_{PS}={\vec {v}}_{PS'}+{\vec {v}}_{S'S}$, $\,{\vec {v}}_{PC}={\vec {v}}_{PA}+{\vec {v}}_{AB}+{\vec {v}}_{BC}$, $\,{\vec {a}}_{PS}={\vec {a}}_{PS'}+{\vec {a}}_{S'S}$

Newton's_Laws_of_Motion

Newton's 2^nd Law $\;m{\vec {a}}=d{\vec {p}}/dt=\sum {\vec {F}}_{j}$, where ${\vec {p}}=m{\vec {v}}$ is momentum, $m$ is mass, and $\sum {\vec {F}}_{j}$ is the sum of all forces This sum needs only include external forces because all internal forces cancel by the 3^rd law ${\vec {F}}_{AB}=-{\vec {F}}_{BA}$. The 1^st law is that velocity is constant if the net force is zero.

▭ Weight$={\vec {w}}=m{\vec {g}}$.

▭ normal force is a component of the contact force by the surface. If the only forces are contact and weight, $|{\vec {N}}|=N=mg\cos \theta$ where $\theta$ is the angle of incline.

▭ Hooke's law $F=-kx$ where $k$ is the spring constant.

Applications_of_Newton's_Laws

$f_{s}\leq \mu _{s}N{\text{ and }}f_{k}=\mu _{k}N$: $\,f=$ friction, $\mu _{s,k}=$ coefficient of (static,kinetic) friction, $N=$ normal force.

▭ Centripetal force$F_{c}=mv^{2}/r=mr\omega ^{2}$ for uniform circular motion. Angular velocity $\omega$ is measured in radians per second.

▭ Ideal angle of banked curve: $\tan \theta =v^{2}/(rg)$ for curve of radius $r$ banked at angle $\theta$.

▭ Drag equation $F_{D}={\tfrac {1}{2}}C\rho Av^{2}$ where $C=$ Drag coefficient, $\rho =$ mass density, $A=$ area, $v=$ speed. Holds approximately for large Reynold's number $=\mathrm {Re} =\rho vL/\eta$, where $\eta =$dynamic viscosity; $L=$ characteristic length.

▭ Stokes's law models a sphere of radius $r$ at small Reynold's number: $F_{s}=6\pi r\eta v$.

Work_and_Kinetic_Energy

Infinitesimal work done by force: $dW={\vec {F}}\cdot d{\vec {r}}=|{\vec {F}}|\,|d{\vec {r}}|\cos \theta$ leads to the path integral $W_{AB}=\int _{A}^{B}{\vec {F}}\cdot d{\vec {r}}$

▭ Work done from A→B by friction $-f_{k}|\ell _{AB}|,\;$gravity $-mg(y_{B}-y_{A}),\;$ and spring $-{\tfrac {1}{2}}k\left(x_{B}^{2}-x_{A}^{2}\right)$

▭ Work-energy theorem: The work done on a particle is $W_{net}=K_{B}-K_{A}$ where kinetic energy $=K={\tfrac {1}{2}}mv^{2}={\frac {p^{2}}{2m}}$.

▭ Power$=P=dW/dt={\vec {F}}\cdot {\vec {v}}$.

Potential_Energy_and_Conservation_of_Energy

Potential Energy: $\Delta U_{AB}=U_{B}-U_{A}=-W_{AB}$; PE at ${\vec {r}}$ WRT ${\vec {r}}_{0}$ is $\Delta U=U({\vec {r}})-U({\vec {r}}_{0})$

$U=mgy+{\mathcal {C}}$ (gravitational PE Earth's surface. $U={\tfrac {1}{2}}kx^{2}+{\mathcal {C}}$ (ideal spring)

▭ Conservative force: $\oint {\vec {F}}_{\text{cons}}\cdot d{\vec {r}}=0$. In 2D, ${\vec {F}}(x,y)$ is conservative if and only if ${\vec {F}}=-(\partial U/\partial x)\,{\hat {i}}-(\partial U/\partial y)\,{\hat {j}}\iff \partial F_{x}/\partial y=\partial F_{y}/\partial x$

▭ Mechanical energy is conserved if no non-conservative forces are present: $0=W_{nc,AB}=\Delta (K+U)_{AB}=\Delta E_{AB}$

Linear_Momentum_and_Collisions

${\vec {F}}(t)=d{\vec {p}}/dt{\text{, where }}{\vec {p}}=m{\vec {v}}$ is momentum.

▭ Impulse-momentum theorem ${\vec {J}}=F_{ave}\Delta t=\int _{t_{i}}^{t_{f}}{\vec {F}}dt=\Delta {\vec {p}}$.

▭ For 2 particles in 2D ${\text{If }}{\vec {F}}_{ext}=0{\text{ then }}\sum _{j=1}^{N}{\vec {p}}_{j}=0\Rightarrow p_{f,\alpha }=p_{1,i,\alpha }+p_{2,i,\alpha }$ where (α,β)=(x,y)

▭ Center of mass: ${\vec {r}}_{CM}={\tfrac {1}{M}}\sum _{j=1}^{N}m_{j}{\vec {r}}_{j}\rightarrow {\tfrac {1}{M}}\int {\vec {r}}dm,$ ${\vec {v}}_{CM}={\tfrac {\,d}{dt}}{\vec {r}}_{CM}$, and ${\vec {p}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {v}}_{j}=M{\vec {v}}_{CM}.$

▭ ${\vec {F}}={\tfrac {\,d}{dt}}{\vec {p}}_{CM}=m{\vec {a}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {a}}_{j}$

▭ Rocket equation $mdv=-udm\Rightarrow \Delta v=u\ln(m_{f}/m_{i})$ where u is the gas speed WRT the rocket.

Fixed-Axis_Rotation

$\theta =s/r\,$ is angle in radians,$\,\omega =d\theta /dt\,$ is angular velocity;

▭ $\,v_{t}=\omega r=ds/dt\,$ is tangential speed. Angular acceleration is $\alpha =d\omega /dt=d^{2}\theta /dt^{2}\,$. $a_{t}=\alpha r=d^{2}s/dt^{2}\,$ is the tangential acceleration.

▭ Constant angular acceleration ${\bar {\omega }}={\tfrac {1}{2}}(\omega _{0}+\omega _{f})\,$ is average angular velocity.

▭ $\theta _{f}=\theta _{0}+{\bar {\omega }}t=\theta _{0}+\omega _{0}t+{\tfrac {1}{2}}\alpha t^{2}\,.$

▭ $\omega _{f}=\omega _{0}+\alpha t.\,$ $\omega _{f}^{2}=\omega _{0}^{2}+2\alpha \Delta \theta \,.$

▭ Total acceleration is centripetal plus tangential: ${\vec {a}}={\vec {a}}_{c}+{\vec {a}}_{t}.\,$

▭ Rotational kinetic energy is $K={\tfrac {1}{2}}I\omega ^{2},\,$ where $I=\sum _{j}m_{j}r_{j}^{2}\rightarrow \int r^{2}dm$ is the Moment of inertia.

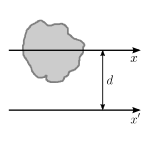
▭ parallel axis theorem $I_{parallel-axis}=I_{center\,of\,mass}+md^{2}$

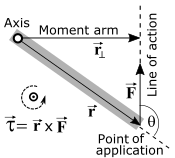
▭ Restricting ourselves to fixed axis rotation, $r$ is the distance from a fixed axis; the sum of torques, ${\vec {\tau }}={\vec {r}}\times {\vec {F}}$ requires only one component, summed as $\tau _{net}=\sum \tau _{j}=\sum r_{\perp _{j}}F_{j}=I\alpha$.

▭ Work done by a torque is $dW=\left(\sum \tau _{j}\right)d\theta$. The Work-energy theorem is $K_{B}-K_{A}=W_{AB}=\int _{\theta _{A}}^{\theta _{B}}\left(\sum _{j}\tau _{j}\right)d\theta$.

▭ Rotational power $=P=\tau \omega$.

I=∫r²dm for a hoop, disk, cylinder, box, plate, rod, and spherical shell or solid can be found from this figure.

Angular_Momentum

Center of mass (rolling without slip) $d_{CM}=r\theta ,\;$ $v_{CM}=r\omega ,\;$$a_{MC}=R\alpha ={\tfrac {mg\sin \theta /}{m+\left(I_{cm}/r^{2}\right)}}$

▭ Total angular momentum and net torque: $d{\vec {L}}/dt=\sum {\vec {\tau }}$ $={\vec {l}}_{1}+{\vec {l}}_{2}+...;$ ${\vec {l}}={\vec {r}}\times {\vec {p}}\,$ for a single particle. $L_{total}=I\omega .$

▭ Precession of a top $\omega _{P}=mrg/(I\omega ).$

Static_Equilibrium_and_Elasticity

Equilibrium $\sum {\vec {F}}_{j}=0=\sum {\vec {\tau }}_{j}.\,$ Stress = elastic modulus · strain (analogous to Force = k · Δ x )

▭ (Young's , Bulk , Shear) modulus: $\left({\tfrac {F_{\perp }}{A}}=Y\cdot {\tfrac {\Delta L}{L_{0}}}\,,\;\Delta p=B\cdot {\tfrac {-\Delta V}{V_{0}}}\,,\;{\tfrac {F_{\parallel }}{A}}=S\cdot {\tfrac {\Delta x}{L_{0}}}\right)$

Gravitation

Newton's law of gravity ${\vec {F}}_{12}=G{\tfrac {m_{1}m_{2}}{r^{2}}}{\hat {r}}_{12}$

▭ Earth's gravity $g=G{\tfrac {M_{E}}{r^{2}}}$

▭ Gravitational PE beyond Earth $U=-G{\tfrac {M_{E}m}{r}}$

▭ Energy conservation ${\tfrac {1}{2}}mv_{1}^{2}-G{\tfrac {Mm}{r_{1}}}={\tfrac {1}{2}}mv_{2}^{2}-G{\tfrac {Mm}{r_{2}}}$

▭ Escape velocity $v_{esc}={\sqrt {\tfrac {2GM_{E}}{r}}}$

▭ Orbital speed $v_{orbit}={\sqrt {\tfrac {GM_{E}}{r}}}$

▭ Orbital period $T=2\pi {\sqrt {\tfrac {r^{3}}{GM_{E}}}}$

▭ Energy in circular orbit $E=K+U=-{\tfrac {GmM_{E}}{2r}}$

▭ Conic section ${\tfrac {\alpha }{r}}=1+e\,\!\cos \theta$

▭ Kepler's third law $T^{2}={\tfrac {4\pi ^{2}}{GM}}a^{3}$

▭ Schwarzschild radius $R_{S}={\tfrac {2GM}{c^{2}}}$

Fluid_Mechanics

Mass density $\rho =m/V\;$ ▭ Pressure $P=F/A\;$

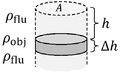
Pressure is the weight per unit area of the fluid above a point.

• The buoyant force $B$ equals the weight of the displaced fluid. If $W$ is the weight of a cylindrical object, the displaced volume is $A\Delta h$ and:

   ▭ $B=\rho _{flu}(A\Delta h)g$ and ▭ $W=\rho _{obj}(A\Delta h)g=M_{obj}g$

▭ Pressure vs depth/height (constant density)$\,p=p_{o}+\rho gh\Leftarrow dp/dy=-\rho g$

▭ Absolute vs gauge pressure $\,p_{abs}=p_{g}+p_{atm}\;$

▭ Pascal's principle: $\,F/A\,$ depends only on depth, not on orientation of A.

▭ Volume flow rate $Q=dV/dt\;$

▭ Continuity equation $\rho _{1}A_{1}v_{1}=\rho _{2}A_{2}v_{2}$$\Rightarrow A_{1}v_{1}=A_{2}v_{2}{\text{ if }}\rho =const.\;$

▭ Bernoulli's principle $p_{1}+{\tfrac {1}{2}}\rho v_{1}^{2}+\rho gy_{1}=p_{2}+{\tfrac {1}{2}}\rho v_{2}^{2}+\rho gy_{2}$

▭ Viscosity $\eta ={\tfrac {FL}{vA}}$ where F is the force applied by a fluid that is moving along a distance L from an area A.

▭ Poiseuille equation $p_{2}-p_{1}=QR$ where $R={\tfrac {8\eta \ell }{\pi r^{4}}}$ is "resistance" for a pipe of radius $r$ and length $\ell$.

Oscillations

Frequency $f$, period $T$ and angular frequency $\omega \,:\;$ $fT=1\,,\quad \omega T=2\pi$

▭ Simple harmonic motion $x(t)=A\cos(\omega t+\phi ),\,$ $v(t)=-A\omega \sin(\omega t+\phi ),\,$ $a(t)=-A\omega ^{2}\cos(\omega t+\phi )$ also models the x-component of uniform circular motion.

▭ For $(A,\omega )$ positive: $\,x_{max}=A,\;v_{max}=A\omega ,\;a_{max}=A\omega ^{2}$

▭ Mass-spring $\omega =2\pi /T=2\pi f={\sqrt {k/m}};\,$

▭ Energy $E_{Tot}={\tfrac {1}{2}}kx^{2}+{\tfrac {1}{2}}mv^{2}={\tfrac {1}{2}}mv_{max}^{2}={\tfrac {1}{2}}kx_{max}^{2}\Rightarrow$$v=\pm {\sqrt {{\tfrac {k}{m}}\left(A^{2}-x^{2}\right)}}$

▭ Simple pendulum $\omega \approx {\sqrt {g/L}}$

▭ Physical pendulum $\tau =-MgL\sin \theta \approx -MgL\theta \Rightarrow \;$$\omega ={\sqrt {mgL/I}}$ and $L$ measures from pivot to CM.

▭ Torsional pendulum $\tau =-\kappa \theta$$\Rightarrow \omega ={\sqrt {I/\kappa }}$

▭ Damped harmonic oscillator $m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}$$\Rightarrow x=A_{0}e^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}$ where $\omega ={\sqrt {\omega _{0}^{2}-\left({\tfrac {b}{2m}}\right)^{2}}}$ and $\omega _{0}={\sqrt {\tfrac {k}{m}}}.$

▭ Forced harmonic oscillator (MIT wiki!) $m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}+F_{0}\sin \omega t$$\Rightarrow x=Ae^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}$ where $A={\tfrac {F_{0}}{\sqrt {m^{2}(\omega -\omega _{0})^{2}+b^{2}\omega ^{2}}}}$.

Waves

Wave speed (phase velocity) $v=\lambda /T=\lambda f=\omega /k$ where $k=2\pi /\lambda$ is wavenumber.

▭ Wave and pulse speed of a stretched string $={\sqrt {F_{T}/\mu }}$ where $F_{T}$ is tension and $\mu$ is linear mass density.

▭ Speed of a compression wave in a fluid $v={\sqrt {B/\rho }}.$

▭ Periodic travelling wave $y(x,t)=A\sin(kx\mp \omega t)$ travels in the positive/negative direction. The phase is $kx\mp \omega t$ and the amplitude is $A$.

▭ The resultant of two waves with identical amplitude and frequency $y_{R}(x,t)=\left[2A\cos \left({\tfrac {\phi }{2}}\right)\right]\sin \left(kx-\omega t+{\tfrac {\phi }{2}}\right)$ where $\phi$ is the phase shift.

▭ This wave equation $\partial ^{2}y/\partial t^{2}=v_{w}^{2}\,\partial ^{2}y/\partial x^{2}$ is linear in $y=y(x,t)$

▭ Power in a tranverse stretched string wave $P_{ave}={\tfrac {1}{2}}\mu A^{2}\omega ^{2}v$.

▭ Intensity of a plane wave $I=P/A\Rightarrow {\tfrac {P}{4\pi r^{2}}}$ in a spherical wave.

▭ Standing wave $y(x,t)=A\sin(kx)\cos(\omega t+\phi )$ For symmetric boundary conditions $\lambda _{n}=2\pi /k_{n}={\tfrac {2}{\pi }}L$ $n=1,2,3,...$, or equivalently $f=nf_{1}$ where $f_{1}={\tfrac {v}{2L}}$ is the fundamental frequency.

Sound

Pressure and displacement fluctuations in a sound wave $P=\Delta P_{max}\sin(kx\mp \omega t+\phi )$ and $s=s_{max}\cos(kx\mp \omega t+\phi )$

▭ Speed of sound in a fluid $v=f\lambda ={\sqrt {\beta /\rho }}$, ▭ in a solid ${\sqrt {Y/\rho }}$, ▭ in an idal gas ${\sqrt {\gamma RT/M}}$, ▭ in air $331{\tfrac {m}{s}}{\sqrt {\tfrac {T_{K}}{273\,K}}}=331{\tfrac {m}{s}}{\sqrt {1+{\tfrac {T_{C}}{273^{o}C}}}}$

▭ Decreasing intensity spherical wave $I_{2}=I_{1}\left({\tfrac {r_{1}}{r_{2}}}\right)^{2}$

▭ Sound intensity $I={\tfrac {\langle P\rangle }{A}}={\tfrac {\left(\Delta P_{max}\right)^{2}}{2\rho v}}$ ▭  ...level $10\log _{10}{I/I_{0}}$

▭ Resonance tube One end closed: $\lambda _{n}={\tfrac {4}{n}}L,$ $f_{n}=n{\tfrac {v}{4L}},$ $n=1,3,5,...$ ▭ Both ends open: $\lambda _{n}={\tfrac {2}{n}}L,$ $f_{n}=n{\tfrac {v}{2L}},$ $n=1,2,3,...$

▭ Beat frequency $f_{beat}=|f_{2}-f_{1}|$

▭ (nonrelativistic) Doppler effect $f_{o}=f_{s}{\tfrac {v\pm v_{o}}{v\mp v_{s}}}$ where $v$ is the speed of sound, $v_{s}$ is the velocity of the source, and $v_{o}$ is the velocity of the observer.

▭ Angle of shock wave $\sin \theta =v/v_{s}=1/M$ where $v$ is the speed of sound, $v_{s}$ is the speed of the source, and $M$ is the Mach number.