Wright State University Lake Campus/University Physics Volume 1/Equations

Material customized for the first semester course at WSU Lake in green

Math

radian&arclength

Metric prefixes on page 5.

▭ Arclength $s$ ▭ $r$ radius
▭ $\theta =s/r$ (in radians)
▭ $C_{\odot }=\,2\pi r$ Circumference of circle
▭ $A_{\odot }=\,\pi r^{2}$ Area of circle
▭ $A_{\bigcirc }=4\pi r^{2}$ Area of sphere
▭ $V_{\bigcirc }={\frac {4}{3}}\pi r^{3}$ Volume of sphere
▭ ${\vec {\mathcal {F}}}\cdot d{\vec {s}}$ $={\mathcal {F}}_{x}dx+{\mathcal {F}}_{y}dy={\mathcal {F}}_{r}dr+{\mathcal {F}}_{\theta }rd\theta$

Mechanics

Symbols

▭ ${\vec {r}}=x{\hat {i}}+y{\hat {j}}+z{\hat {k}}=x{\hat {x}}+y{\hat {y}}+z{\hat {z}}$ Position
▭ $\Delta {\vec {\ell }},d{\vec {\ell }},\Delta {\vec {s}},d{\vec {s}}$ Line element (better than $d{\vec {r}}$ )
▭ ${\vec {v}}=d{\vec {r}}/dt$ Velocity [m/s]
▭ ${\vec {a}}=d{\vec {v}}/dt$ Acceleration [m/s]
▭ ${\vec {F}}=m{\vec {a}}$ Force [N], Mass [kg], Acceleration [m/s²]
▭ $f$ Friction force [N] or frequency [Hz=s⁻¹]
▭ $\mu _{s,k}$ (static, kinetic) coefficient of friction
▭ ${\vec {N}}$ normal force
▭ $g$ gravitational constant (Earth: 9.8m/s²)
Universal gravitational constant G≈6.67×10⁻¹¹
m³·kg⁻¹·s⁻²
▭ $W$ Work [J=Nm=kg(m/s)²]
▭ $P$ Power [W=J/s]
▭ ${\vec {p}}$ Momentum
▭ $p$ Pressure (N/m²)
▭ $KE(PE)$ Kinetic (Potential) Energy [J=Nm=Ws]
▭ $(U_{g},U_{s})$ Potential energy (gravity, spring)
▭ $F=-k_{s}x$ defines spring constant [N/m]
▭ $T$ Tension [N] or period [s] or temperature [K]
▭ $Q$ Heat [J=Ws]
▭ $\theta$ Angle (radians)
▭ $\omega =d\theta /dt$ Angular velocity (speed) [s⁻¹]
▭ $\alpha =d\omega /dt$ Angular acceleration [s⁻²]
▭ $I=\Sigma m_{i}r_{i}^{2}$ Moment of inertia
▭ $\tau =I\alpha$ Torque ▭ $L=I\omega$ Angular momentum

Kinematics

Linear motion	Rotational motion	Defining equation
Displacement = $\mathbf {x}$	Angular displacement = $\theta$	$\theta =\mathbf {s} /\mathbf {r}$
Velocity = $\mathbf {v}$	Angular velocity = $\omega$	$\omega =\mathbf {d} \theta /\mathbf {dt} =\mathbf {v} /\mathbf {r}$
Acceleration = $\mathbf {a}$	Angular acceleration = $\alpha$	$\alpha =\mathbf {d} \omega /\mathbf {dt} =\mathbf {a_{\mathbf {t} }} /\mathbf {r}$
Mass = $\mathbf {m}$	Moment of Inertia = $\mathbf {I}$	$\mathbf {I} =\sum \mathbf {m_{j}} \mathbf {r_{j}} ^{2}$
Force = $\mathbf {F} =\mathbf {m} \mathbf {a}$	Torque = $\tau =\mathbf {I} \alpha$	$\tau =\sum \mathbf {r_{j}} \mathbf {F} _{\perp }\mathbf {_{j}} =\sum \mathbf {r_{\perp j}} \mathbf {F} _{\mathbf {_{j}} }$
Momentum= $\mathbf {p} =\mathbf {m} \mathbf {v}$	Angular momentum= $\mathbf {L} =\mathbf {I} \omega$	$\mathbf {L} =\sum \mathbf {r_{j}} \mathbf {p} \mathbf {_{j}}$
Kinetic energy = ${\frac {1}{2}}\mathbf {m} \mathbf {v} ^{2}$	Kinetic energy = ${\frac {1}{2}}\mathbf {I} \omega ^{2}$	${\frac {1}{2}}\sum \mathbf {m_{j}} \mathbf {v_{j}} ^{2}={\frac {1}{2}}\sum \mathbf {m_{j}} \mathbf {r_{j}} ^{2}\omega ^{2}$

Vector notation	Component notation
${\vec {r}}-{\vec {r}}_{0}={\vec {v}}_{0}t+{\frac {1}{2}}{\vec {a}}t^{2}$	${\vec {v}}_{0}={\vec {v}}_{0x}{\hat {i}}+{\vec {v}}_{0y}{\hat {j}}+{\vec {v}}_{0z}{\hat {k}}$
$v^{2}=v_{0}^{2}+2{\vec {a}}\cdot ({\vec {r}}-{\vec {r}}_{0})\,$	Free fall: $a_{x}=0,\;a_{y}=-g$

Linear motion	Angular motion
$x-x_{0}=v_{0}t+{\frac {1}{2}}at^{2}$	$\theta -\theta _{0}=\omega _{0}t+{\frac {1}{2}}\alpha t^{2}$
$v=v_{0}+at\,$	$\omega =\omega _{0}+\alpha t\,$
$x-x_{0}={\frac {1}{2}}(v_{0}+v)t$	$\theta -\theta _{0}={\frac {1}{2}}(\omega _{0}+\omega )t$
$v^{2}=v_{0}^{2}+2a(x-x_{0})\,$	$\omega ^{2}=\omega _{0}^{2}+2\alpha (\theta -\theta _{0})$

Equations

▭ $KE={\frac {1}{2}}mv^{2}\,$ ▭ $U_{g}=mgy+{\mathcal {C}}$ ▭ $U_{s}={\frac {1}{2}}k_{s}x^{2}$
▭ $\sum KE_{f}+\sum PE_{f}=\sum KE_{i}+\sum PE_{i}-Q$
▭ $W=F\ell \cos \theta ={\vec {F}}\cdot {\vec {\ell }}\Rightarrow \sum {\vec {F}}\cdot \Delta \ell \Rightarrow \int {\vec {F}}\cdot \Delta \ell$
▭ $P={\frac {{\vec {F}}\cdot {\vec {\Delta }}\ell }{\Delta t}}={\vec {F}}\cdot {\vec {v}}$ is power
▭ ${\vec {p}}=m{\vec {v}}$ Momentum
▭ $\sum {\vec {p}}_{f}=\sum {\vec {p}}_{f}+\int {\vec {F}}_{ext}dt$
▭ $m_{1}v_{1}+m_{2}v_{2}=(m_{1}+m_{2})v_{f}$ Inelastic collision
▭ $\omega T=2\pi \Leftrightarrow fT=1$ frequency-period
▭ $a=v^{2}/r=\omega v=\omega ^{2}r$ centripetal acceleration
▭ $\sum {\vec {F}}_{j}=0=\sum {\vec {\tau }}_{j}$ $\tau =rF_{\perp }$ statics
▭ $f_{s}\leq \mu _{s}N,\;f_{k}=\mu _{k}N$ friction
▭ ${\vec {F}}_{12}=G{\tfrac {m_{1}m_{2}}{r^{2}}}{\hat {r}}_{12}$ Newtonian gravity
▭ ${\vec {F}}_{12}=G{\tfrac {m_{1}m_{2}}{r^{2}}}{\hat {r}}_{12}$ Newtonian gravity
▭ $g=G{\tfrac {M}{r^{2}}}$ planet's surface gravity

Fluid_Mechanics

▭ Mass density $\rho =m/V\;$

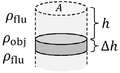
▭ Pressure $P=F/A\;$

Buoyant force $B$ equals weight of the displaced fluid. If $W$ is the weight of a cylindrical object, the displaced volume is $A\Delta h$

▭ $B=\rho _{flu}(A\Delta h)g$ and ▭ $W=\rho _{obj}(A\Delta h)g=M_{obj}g$

▭ Pressure vs depth/height (constant density) $\,p=p_{o}+\rho gh\Leftarrow dp/dy=-\rho g$

▭ Volume flow rate $Q=dV/dt\;$

▭ Continuity equation $\rho _{1}A_{1}v_{1}=\rho _{2}A_{2}v_{2}$ $\Rightarrow A_{1}v_{1}=A_{2}v_{2}{\text{ if }}\rho =const.\;$

▭ Bernoulli's principle $p_{1}+{\tfrac {1}{2}}\rho v_{1}^{2}+\rho gy_{1}=p_{2}+{\tfrac {1}{2}}\rho v_{2}^{2}+\rho gy_{2}$

Oscillations

▭ Simple harmonic motion $x(t)=A\cos(\omega t+\phi ),\,$ $v(t)=-A\omega \sin(\omega t+\phi ),\,$ $a(t)=-A\omega ^{2}\cos(\omega t+\phi )$

▭ $\,x_{max}=A,\;v_{max}=A\omega ,\;a_{max}=A\omega ^{2}$ , where $\omega ={\sqrt {k/m}};\,$ and $k$ is spring constant

▭ Energy $E_{Tot}={\tfrac {1}{2}}kx^{2}+{\tfrac {1}{2}}mv^{2}={\tfrac {1}{2}}mv_{max}^{2}={\tfrac {1}{2}}kx_{max}^{2}$

Physics of hearing (extracted from Physics equations)

$v_{s}={\sqrt {\frac {T}{273}}}\cdot 331{\text{m/s}}$ speed of sound (T in Kelvins). $v_{s}={\sqrt {\frac {\gamma k_{B}T}{m}}}$ where $\gamma \approx 1.4$
$v={\sqrt {\frac {F}{\mu }}}$ Speed of a stretched string wave: $F$ is the tension and $\mu$ is the linear mass density (kilograms per meter).

$f\lambda =v_{p}$ relates the frequency, f, wavelength, λ,and the the phase speed, v_p of the wave (also written as v_w) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
$L={\frac {n\lambda _{n}}{2}}$ describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.
Beat frequency: The frequency of beats heard if two closely space frequencies, $f_{1}$ and $f_{2}$ , are played is $\Delta f=|f_{2}-f_{1}|$ .
Musical acoustics: Frequency ratios of 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 8/5 are called the (just) "octave", "fifth", "fourth", "major-sixth", "major-third", "minor-third", and "minor-sixth", respectively.

Thermodynamics

Constants and conversions

Boltzmann's constant = k_B≈ 1.38 × 10^-23 J K⁻¹ , and the gas constant is R = N_Ak_B≈8.314 J K⁻¹ mol⁻¹, where N_A≈ 6.02 × 10²³ is the Avogadro number.
Boltzmann's constant can also be written in eV and Kelvins: k_B ≈8.6 × 10^-5 eV/deg, where 1eV=1.602x10⁻¹⁹ Joules
$T_{C}=T_{K}-273.15$ converts from Celsius to Kelvins, and $T_{F}={\frac {9}{5}}T_{C}+32$ converts from Celsius to Fahrenheit.
1 amu = 1 u ≈ 1.66 × 10^-27 kg is the approximate mass of a proton or neutron.

13-Temperature, Kinetic Theory, and Gas Laws

$PV=nRT=Nk_{B}T$ is the ideal gas law, where P is pressure, V is volume, n is the number of moles and N is the number of atoms or molecules. Temperature is in Kelvins.

${\frac {3}{2}}k_{B}T={\frac {1}{2}}mv_{rms}^{2}$ is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
$v_{rms}={\sqrt {\frac {3k_{B}T}{m}}}={\sqrt {\overline {v^{2}}}}$ is the root-mean-square speed of atoms in an ideal gas.

14-Heat and Heat Transfer

Here it is convenient to define heat as energy that passes between two objects of different temperature $Q$ The SI unit is the Joule. The rate of heat trasfer, $\Delta Q/\Delta t$ or ${\dot {Q}}$ is "power": 1 Watt = 1 W = 1J/s

$Q=mc_{S}\Delta T$ is the heat required to change the temperature of a substance of mass, m. The change in temperature is ΔT. The specific heat, c_S, depends on the substance (and to some extent, its temperature and other factors such as pressure). Heat is the transfer of energy, usually from a hotter object to a colder one. The units of specfic heat are energy/mass/degree, or J/(kg-degree).
$Q=mL$ is the heat required to change the phase of a a mass, m, of a substance (with no change in temperature). The latent heat, L, depends not only on the substance, but on the nature of the phase change for any given substance. L_F is called the latent heat of fusion, and refers to the melting or freezing of the substance. L_V is called the latent heat of vaporization, and refers to evaporation or condensation of a substance.
${\dot {Q}}={\frac {k_{c}A}{d}}\Delta T$ is rate of heat transfer for a material of area, A. The difference in temperature between two sides separated by a distance, d, is $\Delta T$ . The thermal conductivity, k_c, is a property of the substance used to insulate, or subdue, the flow of heat.

15-Thermodynamics

Here, Pressure (P), Energy (E), Volume (V), and Temperature (T) are the state functions.

The net work done per cycle is the area enclosed by the loop and equals the net heat flow into the system, $Q_{in}-Q_{out}$ (valid only for closed loops).
$\Delta W=-F\Delta x=(-P\cdot \mathrm {Area} )\left({\frac {\Delta V}{\mathrm {Area} }}\right)=-P\Delta V$ is the work done on a system of pressure P by a piston of voulume V. If ΔV>0 the substance is expanding as it exerts an outward force, so that ΔW<0 and the substance is doing work on the universe; ΔW>0 whenever the universe is doing work on the system.
$\Delta Q$ is the amount of heat (energy) that flows into a system. It is positive if the system is placed in a heat bath of higher temperature. If this process is reversible, then the heat bath is at an infinitesimally higher temperature and a finite ΔQ takes an infinite amount of time.
$\Delta E=\Delta Q-P\Delta V$ is the change in energy (First Law of Thermodynamics).
$-\int P\ dV$ is work done on system. $\oint P\ dV=Q_{in}-Q_{out}$ is work (out) per cycle.

Original (long) formula sheet

OpenStax University Physics Volume 1/Equations (master)

The circumference of a circle is $C_{\odot }=\,2\pi r$ and the circle's area is $A_{\odot }=\,\pi r^{2}$ is its area.
The surface area of a sphere is $A_{\bigcirc }=4\pi r^{2}$ and sphere's volume is $V_{\bigcirc }={\frac {4}{3}}\pi r^{3}$
1 kilometer = .621 miles and 1 MPH = 1 mi/hr ≈ .447 m/s
Typical air density is 1.2kg/m³, with pressure 10⁵Pa. The density of water is 1000kg/m³.
Earth's mean radius ≈ 6371km, mass ≈ 6×10²⁴
kg
Universal gravitational constant = G ≈ 6.67×10⁻¹¹
m³·kg⁻¹·s⁻²
Speed of sound ≈ 340m/s and the speed of light = c ≈ 3×10⁸m/s
One light-year ≈ 9.5×10¹⁵m ≈ 63240AU (Astronomical unit)
1 amu (or 1 u) ≈ 1.66 × 10^-27 kg is the approximate mass of a proton or neutron.... <These 8 equations were added for WSU-L exams>

OpenStax University Physics Volume 1/Equations (master) OpenStax University Physics Volume 1/Equations (master) OpenStax University Physics Volume 1/Equations (master) OpenStax University Physics Volume 1/Equations (master)

This is a transclusion, added two days before Test 1

$x=x_{0}+v_{0x}\Delta t+{\frac {1}{2}}a_{x}\Delta t^{2}$	$v_{x}=v_{0x}+a_{x}\Delta t$	$v_{x}^{2}=v_{x0}^{2}+2a_{x}\Delta x$
$y=y_{0}+v_{0y}\Delta t+{\frac {1}{2}}a_{y}\Delta t^{2}$	$v_{y}=v_{0y}+a_{y}\Delta t$	$v_{y}^{2}=v_{x0}^{2}+2a_{y}\Delta y$

$v^{2}=v_{0}^{2}+2a_{x}\Delta x+2a_{y}\Delta y$ ...in advanced notation this becomes $\Delta (v^{2})=2{\vec {a}}\cdot \Delta {\vec {\ell }}$ .

In free fall we often set, a_x=0 and a_y= -g. If angle is measured with respect to the x axis:

$v_{x}=v\cos \theta$ $v_{y}=v\sin \theta$ $v_{x0}=v_{0}\cos \theta _{0}$ $v_{y0}=v_{0}\sin \theta _{0}$

OpenStax University Physics Volume 1/Equations (master)

Use for this quiz

OpenStax University Physics Volume 1/Equations (master)

The x and y components of the three forces of tension on the small grey circle where the three "massless" ropes meet are:

T_{1x}=-T_{1}\cos \theta _{1}

,

T_{1y}=T_{1}\sin \theta _{1}

T_{2x}=0

,

T_{2y}=-mg

T_{3x}=T_{3}\cos \theta _{3}

,

T_{3y}=T_{3}\sin \theta _{3}

Also transcluded from Physics equations

$2\pi \;rad=360\;deg=1\;rev$ relates the radian, degree, and revolution.
$f={\frac {\#\,{\text{revs}}}{\#\,{\text{secs}}}}$ is the number of revolutions per second, called frequency.
$T={\frac {\#\,{\text{secs}}}{\#\,{\text{revs}}}}$ is the number of seconds per revolution, called period. Obviously $fT=1$ .
$\omega ={\frac {\Delta \theta }{\Delta t}}$ is called angular frequency (ω is called omega, and θ is measured in radians). Obviously $\omega T=2\pi$
$a={\frac {v^{2}}{r}}=\omega v=\omega ^{2}r$ is the acceleration of uniform circular motion, where v is speed, and r is radius.
$v=\omega r=2\pi r/T$ , where T is period.

Sound

Pressure and displacement fluctuations in a sound wave $P=\Delta P_{max}\sin(kx\mp \omega t+\phi )$ and $s=s_{max}\cos(kx\mp \omega t+\phi )$

▭ Speed of sound in a fluid $v=f\lambda ={\sqrt {\beta /\rho }}$ , ▭ in a solid ${\sqrt {Y/\rho }}$ , ▭ in an idal gas ${\sqrt {\gamma RT/M}}$ , ▭ in air $331{\tfrac {m}{s}}{\sqrt {\tfrac {T_{K}}{273\,K}}}=331{\tfrac {m}{s}}{\sqrt {1+{\tfrac {T_{C}}{273^{o}C}}}}$

Physics of hearing (extracted from Physics equations)

$v_{s}={\sqrt {\frac {T}{273}}}\cdot 331{\text{m/s}}$ is the the approximate speed near Earth's surface, where the temperature, T, is measured in Kelvins. A theoretical calculation is $v_{s}={\sqrt {\frac {\gamma k_{B}T}{m}}}$ where $\gamma ={\frac {\varpi +2}{\varpi }}$ for a semi-classical gas with $\varpi$ degrees of freedom. For a diatomic gas such as Nitrogen, γ = 1.4.
$v_{s}={\sqrt {\frac {F}{\mu }}}$ is the speed of a wave in a stretched string if $F$ is the tension and $\mu$ is the linear mass density (kilograms per meter).

$f\lambda =v_{p}$ relates the frequency, f, wavelength, λ,and the the phase speed, v_p of the wave (also written as v_w) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
$L={\frac {n\lambda _{n}}{2}}$ describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.
Beat frequency: The frequency of beats heard if two closely space frequencies, $f_{1}$ and $f_{2}$ , are played is $\Delta f=|f_{2}-f_{1}|$ .
Musical acoustics: Frequency ratios of 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 8/5 are called the (just) "octave", "fifth", "fourth", "major-sixth", "major-third", "minor-third", and "minor-sixth", respectively.

Kinetic theory of gasses

$T_{C}=T_{K}-273.15$ converts from Celsius to Kelvins, and $T_{F}={\frac {9}{5}}T_{C}+32$ converts from Celsius to Fahrenheit.
$PV=nRT=Nk_{B}T$ is the ideal gas law, where $P$ is pressure, $V$ is volume, $n$ is the number of moles and $N$ is the number of atoms or molecules. Temperature must be measured on an absolute scale (e.g. Kelvins).
Boltzmann's constant = $k_{B}$ ≈ 1.38 × 10^-23 J K⁻¹ , and the gas constant is $R=N_{A}k_{B}$ ≈8.314 J K⁻¹ mol⁻¹, where $N_{A}$ ≈ 6.02 × 10²³ is the Avogadro number. Boltzmann's constant can also be written in eV and Kelvins: k_B ≈8.6 × 10^-5 eV/deg.
${\frac {3}{2}}k_{B}T={\frac {1}{2}}mv_{rms}^{2}$ is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
$v_{rms}={\sqrt {\frac {3k_{B}T}{m}}}={\sqrt {\overline {v^{2}}}}$ is the root-mean-square speed of atoms in an ideal gas.
$E={\frac {\varpi }{2}}Nk_{B}T$ is the total energy of an ideal gas, where $\varpi =3\;$ only if the gas is monatomic.

Thermodynamics

Pressure (P), Energy (E), Volume (V), and Temperature (T) are state variables (state functionscalled state functions). The number of particles (N) can also be viewed as a state variable.
Work (W), Heat (Q) are not state variables.
$S(V,T)={\frac {3Nk_{B}}{2}}\ln T+Nk_{B}\ln V+constant$ , is the entropy of an ideal , monatomic gas. The constant is arbitrary only in classical (non-quantum) thermodynamics. Since it is a function of state variables, entropy is also a state function.

A point on a PV diagram define's the system's pressure (P) and volume (V). Energy (E) and pressure (P) can be deduced from equations of state: E=E(V,P) and T=T(V,P). If the piston moves, or if heat is added or taken from the substance, energy (in the form of work and/or heat) is added or subtracted. If the path returns to its original point on the PV-diagram (e.g., 12341 along the rectantular path shown), and if the process is quasistatic, all state variables (P, V, E, T) return to their original values, and the final system is indistinguishable from its original state.

The net work done per cycle is area enclosed by the loop. This work equals the net heat flow into the system, $Q_{in}-Q_{out}$ (valid only for closed loops).

Remember: Area "under" is the work associated with a path; Area "inside" is the total work per cycle.

$\Delta W=-F\Delta x=(-P\cdot \mathrm {Area} )\left({\frac {\Delta V}{\mathrm {Area} }}\right)=-P\Delta V$ is the work done on a system of pressure P by a piston of voulume V. If ΔV>0 the substance is expanding as it exerts an outward force, so that ΔW<0 and the substance is doing work on the universe; ΔW>0 whenever the universe is doing work on the system.
$\Delta Q$ is the amount of heat (energy) that flows into a system. It is positive if the system is placed in a heat bath of higher temperature. If this process is reversible, then the heat bath is at an infinitesimally higher temperature and a finite ΔQ takes an infinite amount of time.
$\Delta E=\Delta Q-P\Delta V$ is the change in energy (First Law of Thermodynamics).

CALCULUS: $\oint P\ dV=Q_{in}-Q_{out}$ .

In an isothermal expansion (contraction), temperature, T, is constant. Hence P=nRT/V and substitution yields,

\int _{Vi}^{Vf}PdV=\int _{Vi}^{Vf}nRT{\frac {dV}{V}}=nRT\int _{Vi}^{Vf}{\frac {dV}{V}}=nRT\ln {\frac {V_{f}}{V_{i}}}