OpenStax University Physics/V2

http://cnx.org/content/col12074/latest/

Temperature and Heat

$T_{C}={\tfrac {5}{9}}\left(T_{F}-32\right)$ relates Celsius to Fahrenheit temperature scales. $T_{K}=T_{C}+273.15$ relates Kelvin to Celsius.

▭ Linear thermal expansion: $\Delta L=\alpha L\Delta T$ relates a small change in length to the total length $L$, where $\alpha$ is the coefficient of linear expansion.
▭ For expansion in two and three dimensions: $\Delta A=2\alpha A\Delta T$ and $\Delta V=\beta V\Delta T$, respectively.
▭ Heat transfer is $Q=mc\Delta T$ where $c$ is the specific heat capacity. In a calorimeter, $Q_{cold}+Q_{hot}=0$
▭ Latent heat due to a phase change is $Q=mL_{f}$ for melting/freezing and $Q=mL_{v}$ for evaporation/condensation.
▭ Heat conduction (power): $P={\tfrac {kA(T_{h}-T_{c})}{d}}$ where $k$ is heat conductivity and $d$ is thickness and $A$ is area.
▭ $P_{net}=\sigma eA\left(T_{2}^{4}-T_{1}^{4}\right)$ is the radiative energy transfer rate where $e$ is emissivity and $\sigma$ is the Stefan–Boltzmann constant.

The Kinetic Theory of Gases

Ideal gas law: Pressure×Volume $=pV=nRT=Nk_{B}T$ where $n$ is the number of moles and $T$ is an absolute temperature.

▭ $N=nN_{A}$ is the number of particles. Gas constant $R$ = 8.3 J K⁻¹/mol
▭ Avegadro's number: $N_{A}$ = 6.02×10²³. Boltzmann's constant: $k_{B}$ = 1.38×10⁻²³J/K.
▭ Van der Waals equation $\left[p+a(nV)^{2}\right](V-nb)=nRT$
▭ RMS speed $v_{rms}={\sqrt {\overline {v^{2}}}}={\sqrt {\tfrac {3RT}{M}}}={\sqrt {\tfrac {3k_{B}T}{m}}}$ where the overline denotes mean, $m$ is a particle's mass and $M$ is the molar mass.
▭ Mean free path $\lambda ={\tfrac {V}{4{\sqrt {2}}\pi r^{2}N}}={\tfrac {k_{B}T}{4{\sqrt {2}}\pi r^{2}p}}=v_{rms}\tau$ where $\tau$ is the mean-free-time
▭ Internal energy of an ideal monatomic gas $E_{int}={\tfrac {3}{2}}Nk_{B}T=N{\overline {K}}$, where ${\overline {K}}=$ average kinetic energy of a particle.
▭ $Q=nC_{V}\Delta T$ defines the molar heat capacity at constant volume.
▭ $C_{V}={\tfrac {d}{2}}R$ for ideal gas with $d$ degrees of freedom
▭ Maxwell–Boltzmann speed distribution $f(v)={\tfrac {4}{\sqrt {\pi }}}\left({\tfrac {m}{2k_{B}T}}\right)^{3/2}v^{2}e^{-mv^{2}/2k_{B}T}$
▭ Average speed ${\bar {v}}={\sqrt {{\tfrac {8}{\pi }}{\tfrac {RT}{M}}}}$ ▭ Peak velocity $v_{p}={\sqrt {\tfrac {2RT}{M}}}$

The First Law of Thermodynamics

(Pressure, volume, temperature) remain constant in an (isobaric, isochoric, isothermal) process. Heat is not transferred in an adiabatic process.

▭ Equation of state $f(p,V,T)=0$ ▭ Work done by a system $W=\int _{V_{1}}^{V_{2}}pdV$
▭ Internal energy $E_{int}=\sum _{i}\left({\overline {K}}_{i}+{\overline {U}}_{i}\right)$ is a sum over all particles of kinetic and potential energies
▭ First law $\Delta E_{int}=Q-W$ (Q is heat going in and W is work done by as shown in the figure)
▭ $C_{p}=C_{V}+R$ is the molar heat capacity at constant volume
▭ $pV^{\gamma }={\text{constant}}$ for an adiabatic process in an ideal gas, where the heat capacity ratio $\gamma =C_{p}/C_{V}$

The Second Law of Thermodynamics

$W=Q_{h}-Q_{c}=$ work done in a heat engine cycle. ▭ Efficiency $=e={\tfrac {W}{Q_{h}}}=1-{\tfrac {Q_{c}}{Q_{h}}}$

▭ Coefficient of performance for a refrigerator $K_{R}={\tfrac {Q_{c}}{W}}={\tfrac {Q_{c}}{Q_{h}-Q_{c}}}$, and heat pump $K_{P}={\tfrac {Q_{h}}{W}}={\tfrac {Q_{h}}{Q_{h}-Q_{c}}}$
▭ Entropy change $\Delta S={\tfrac {Q}{T}}$ (reversible process at constant temperature) $\rightarrow \int _{A}^{B}{\tfrac {dQ}{T}}=S_{B}-S_{A}$
▭ $\oint {\tfrac {dQ}{T}}$ for any cyclic process $\rightarrow \int _{A}^{B}{\tfrac {dQ}{T}}=S_{B}-S_{A}$ is path independent.
▭ $\Delta S\geq 0$ for any closed system. $\lim _{T\to 0}\Delta S=0$ for any isothermal process.

Electric Charges and Fields

Coulomb's Law ${\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {q_{1}q_{2}}{r_{12}^{2}}}{\hat {r}}_{12}$ where the vacuum permittivity $\varepsilon _{0}=$ 8.85×10⁻¹² F/m.

Elementary charge = e = 1.602×10⁻¹⁹C (electrons have charge q=−e and protons have charge q=+e.)

Dipole moment

▭ By superposition, ${\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}Q\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Qi}^{2}}}{\hat {r}}_{Qi}$ where ${\vec {r}}_{Qi}={\vec {r}}_{Q}-{\vec {r}}_{i}$
▭ Electric field ${\vec {F}}=Q{\vec {E}}$ where ${\vec {E}}({\vec {r}}_{P})={\tfrac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Pi}^{2}}}{\hat {r}}_{Pi}$ is the field at ${\vec {r}}_{P}$ due to charges at ${\vec {r}}_{i}$
▭ The field above an infinite wire ${\vec {E}}(z)={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {2\lambda }{z}}{\hat {k}}$ and above an infinite plane ${\vec {E}}={\tfrac {\sigma }{2\varepsilon _{0}}}{\hat {k}}$
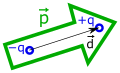
▭ An electric dipole ${\vec {p}}=q{\vec {d}}$ in a uniform electric field experiences the torque $\tau ={\vec {p}}\times {\vec {E}}$

Gauss's Law

 closed .. open

Flux for a uniform electric field $\Phi ={\vec {E}}\cdot {\vec {A}}$ $\to \Phi =\int {\vec {E}}\cdot d{\vec {A}}=\int {\vec {E}}\cdot {\hat {n}}\,dA$ in general.

▭ Closed surface integral $\Phi =\oint {\vec {E}}\cdot d{\vec {A}}=\oint {\vec {E}}\cdot {\hat {n}}\,dA$
▭ Gauss's Law $=q_{enc}=\varepsilon _{0}\oint {\vec {E}}\cdot d{\vec {A}}$. In simple cases: $E\int dA=EA^{*}={\tfrac {q_{enc}}{\varepsilon _{0}}}$
▭ Electric field just outside the surface of a conductor ${\vec {E}}={\tfrac {\sigma }{\varepsilon _{0}}}$

Electric Potential

Electric potential $\Delta V_{AB}=V_{A}-V_{B}=-\int _{A}^{B}{\vec {E}}\cdot d{\vec {\ell }}$. Change in potential energy $=q\Delta V=\Delta U$

▭  Electron (proton) mass = 9.11×10⁻³¹kg (1.67× 10⁻²⁷kg). Electron volt: 1 eV = 1.602×10⁻¹⁹J
▭  Near an isolated point charge $V(r)=k{\tfrac {q}{r}}$ where $k={\tfrac {1}{4\pi \varepsilon _{0}}}$ =8.99×10⁹ N·m/C² is the Coulomb constant.
▭ Work done to assemble N particles $W_{12...N}=\sum _{i=1}^{N}\sum _{j=1}^{i-1}{\tfrac {q_{i}q_{j}}{r_{ij}}}={\tfrac {k}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}{\tfrac {q_{i}q_{j}}{r_{ij}}}{\text{ for }}i\neq j$
▭ Electric potential due to N charges. $V_{P}=k\sum _{1}^{N}{\frac {q_{i}}{r_{i}}}$. For continuous charge $V_{P}=k\int {\frac {dq}{r}}$. For a dipole, $V=k{\tfrac {{\vec {p}}\cdot {\vec {\hat {r}}}}{r^{2}}}$.
▭ Electric field as gradient of potential ${\vec {E}}=-{\tfrac {\partial V}{\partial x}}{\hat {i}}-{\tfrac {\partial V}{\partial y}}{\hat {j}}-{\tfrac {\partial V}{\partial z}}{\hat {k}}=-{\vec {\nabla }}V$ ▭ Del operator^note: Cartesian ${\vec {\nabla }}={\hat {i}}{\tfrac {\partial }{\partial x}}+{\hat {j}}{\tfrac {\partial }{\partial y}}+{\hat {k}}{\tfrac {\partial }{\partial z}}{\text{; }}$Cylindrical ${\vec {\nabla }}={\hat {r}}{\tfrac {\partial }{\partial r}}+{\hat {\phi }}{\tfrac {\partial }{\partial \phi }}+{\hat {z}}{\tfrac {\partial }{\partial z}}{\text{; }}$Spherical ${\vec {\nabla }}={\hat {r}}{\tfrac {\partial }{\partial r}}+{\hat {\theta }}{\tfrac {\partial }{\partial \theta }}+{\hat {\phi }}{\tfrac {\partial }{\partial \phi }}{\text{.}}$

Capacitance

$Q=CV$ defines capacitance. For a parallel plate capacitor, $C=\varepsilon _{0}{\tfrac {A}{d}}$ where A is area and d is gap length.

▭ $4\pi \varepsilon _{0}{\tfrac {R_{1}R_{2}}{R_{2}-R_{1}}}$ and ${\tfrac {2\pi \varepsilon _{0}\ell }{\ln(R_{2}/R_{1})}}$ for a spherical and cylindrical capacitor, respectively
▭ For capacitors in series (parallel) ${\tfrac {1}{C_{S}}}=\sum {\tfrac {1}{C_{i}}}\left(C_{P}=\sum C_{i}\right)$
▭  $u={\tfrac {1}{2}}QV={\tfrac {1}{2}}CV^{2}={\tfrac {1}{2C}}Q^{2}$ ▭ Stored energy density $u_{E}={\tfrac {1}{2}}\varepsilon _{0}E^{2}$
▭ A dielectric with $\kappa >1$ will decrease the capacitor's electric field $E={\tfrac {1}{\kappa }}E_{0}$ and stored energy $U={\tfrac {1}{\kappa }}U_{0}$, but increase the capacitance $C=\kappa C_{0}$ due to the induced electric field ${\vec {E}}_{i}=\left({\tfrac {1}{\kappa }}-1\right){\vec {E}}_{0}$

Current and Resistance

Current (1A=1C/s) $I=dQ/dt=nqv_{d}A$ where $(n,q,v_{d})=$ (density, charge, drift velocity) of the carriers.

▭ $I=JA\rightarrow \int {\vec {J}}\cdot d{\vec {A}}$ , $A$ is the perpendicular area, and $J$ is current density. ${\vec {E}}=\rho {\vec {J}}$ is electric field, where $\rho$ is resistivity.
▭ Resistivity varies with temperature as $\rho =\rho _{0}\left[1+\alpha (T-T_{0})\right]$. Similarily, $R=R_{0}\left[1+\alpha \Delta T\right]$ where $R=\rho {\tfrac {L}{A}}$ is resistance (Ω)
▭ Ohm's law $V=IR$ ▭  Power $=P=IV=I^{2}R=V^{2}/R$

Direct-Current Circuits

Terminal voltage $V_{terminal}=\varepsilon -Ir_{eq}$ where $r_{eq}$ is the internal resistance and $\varepsilon$ is the electromotive force.
▭ Resistors in series and parallel: $R_{series}=\sum _{i=1}^{N}R_{i}$ ▭ $R_{parallel}^{-1}=\sum _{i=1}^{N}R_{i}^{-1}$
▭ Kirchoff's rules. Loop:$\sum I_{in}=\sum I_{out}$ Junction: $\sum V=0$

▭ $V_{terminal}^{series}=\sum _{i=1}^{N}\varepsilon _{i}-I\sum _{i=1}^{N}r_{i}$ ▭ $V_{terminal}^{parallel}=\varepsilon -I\sum _{i=1}^{N}\left({\frac {1}{r_{i}}}\right)^{-1}$ where $r_{i}$ is internal resistance of each voltage source.
▭ Charging an RC (resistor-capacitor) circuit: $q(t)=Q\left(1-e^{-t/\tau }\right)$ and $I=I_{0}e^{-t/\tau }$ where $\tau =RC$ is RC time, $Q=\varepsilon C$ and $I_{0}=\varepsilon /R$.
▭ Discharging an RC circuit: $q(t)=Qe^{-t/\tau }$ and $I(t)=-{\tfrac {Q}{RC}}e^{-t/\tau }$

Magnetic Forces and Fields

• 
  Cross product $|{\vec {a}}\times {\vec {b}}|$$=ab\sin \theta$
• 
  Hall effect ${\vec {v}}_{d}={\vec {E}}\times {\vec {B}}/B^{2}$
• 
  Mass spectrometer in special case that both magnetic fields are equal

▭ ${\vec {F}}=q{\vec {v}}\times {\vec {B}}$ is the force due to a magnetic field on a moving charge.
▭ For a current element oriented along ${\overrightarrow {d\ell }},\;d{\vec {F}}=I{\overrightarrow {d\ell }}\times {\vec {B}}$.

▭ The SI unit for magnetic field is the Tesla: 1T=10⁴ Gauss.
▭ Gyroradius $r={\tfrac {mB}{qB}}.\;$ Period $T={\tfrac {2\pi m}{qB}}.\;$
▭ Torque on current loop ${\vec {\tau }}={\vec {\mu }}\times {\vec {B}}$ where ${\vec {\mu }}=NIA{\hat {n}}$ is the dipole moment. Stored energy $U={\vec {\mu }}\cdot {\vec {B}}.$
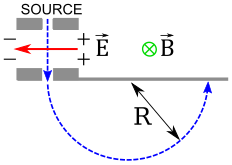
▭ Drift velocity in crossed electric and magnetic fields $v_{d}={\tfrac {E}{B}}$
▭ Hall voltage = $V$ where the electric field is $E=V/\ell =Bv_{d}={\tfrac {IB}{neA}}$
▭ Charge-to-mass ratio $q/m={\tfrac {E}{BB_{0}r}}$ where the $E$ and $B$ fields are crossed and $E=0$ when the magnetic field is $B_{0}$

Sources of Magnetic Fields

▭ Permeability of free space $\mu _{0}=4\pi \times 10^{-7}$ T·m/A
▭ Force between parallel wires ${\tfrac {F}{\ell }}={\tfrac {\mu _{0}I_{1}I_{2}}{2\pi r}}$

▭ Biot–Savart law ${\vec {B}}={\tfrac {\mu _{0}}{4\pi }}\int \limits _{wire}{\frac {Id{\vec {\ell }}\times {\hat {r}}}{r^{2}}}$

▭ Ampère's Law:$\oint {\vec {B}}\cdot d{\vec {\ell }}=\mu _{0}I_{enc}$
▭ Magnetic field due to long straight wire $B={\tfrac {\mu _{0}I}{2\pi R}}$ ▭ At center of loop $B={\tfrac {\mu _{0}I}{2R}}$
▭ Inside a long thin solenoid $B=\mu _{0}nI$ where $n=N/\ell$ is the ratio of the number of turns to the solenoid's length.
▭ Inside a toroid $B={\tfrac {\mu _{0}N}{2\pi r}}$

▭ The magnetic field inside a solenoid filled with paramagnetic material is $B=\mu nI$ where $\mu =(1+\chi )\mu _{0}$ is the permeability

Electromagnetic Induction

Magnetic flux $\Phi _{m}=\int _{S}{\vec {B}}\cdot {\hat {n}}dA$ ▭ Electromotive force $\varepsilon =-N{\tfrac {d\Phi _{m}}{dt,}}$ (Faraday's law)
▭ Motional emf $\varepsilon =B\ell v,$ ▭ rotating coil $NBA\omega \sin \omega t$
▭ Motional emf around circuit $\varepsilon =\oint {\vec {E}}\cdot d{\vec {\ell }}=-{\tfrac {d\Phi _{m}}{dt}}$

Inductance

The SI unit for inductance is the Henry: 1H=1V·s/A ▭ Mutual inductance: $M{\tfrac {dI_{2}}{dt}}=N_{1}{\tfrac {d\Phi _{12}}{dt}}=-\varepsilon _{1}$ where $\Phi _{12}$ is the flux through 1 due to the current in 2 and $\varepsilon _{1}$ is the emf in 1. Likewise, it can be shown^SEE TALK that, $M{\tfrac {dI_{1}}{dt}}=-\varepsilon _{2}$.

▭ Self-inductance $N\Phi _{m}=LI\rightarrow \varepsilon =-L{\tfrac {dI}{dt}}$ ▭  $L_{\text{solenoid}}\approx \mu _{0}N^{2}A\ell ,\,$$L_{\text{toroid}}\approx {\tfrac {\mu _{0}N^{2}h}{2\pi }}\ln {\tfrac {R_{2}}{R_{1}}}.$ Stored energy $U={\tfrac {1}{2}}LI^{2}.$ ▭ $I(t)={\tfrac {\varepsilon }{R}}\left(1-e^{-t/\tau }\right)$is the current in an LR circuit where $\tau =L/R$ is the LR decay time.
▭ The capacitor's charge on an LC circuit $q=q_{0}\cos(\omega t+\phi )$ where $\omega ={\sqrt {\tfrac {1}{LC}}}$ is angular frequency
▭ LRC circuit $q(t)=q_{0}e^{-Rt/2L}\cos(\omega 't+\phi )$ where $\omega '={\sqrt {{\tfrac {1}{LC}}+\left({\tfrac {R}{2L}}\right)^{2}}}$

Alternating-Current Circuits

RLC circiut

AC voltage and current $v=V_{0}\sin(\omega t-\phi )$ if $i=I_{0}\sin \omega t.$
▭ RMS values $I_{rms}={\tfrac {I_{0}}{\sqrt {2}}}$ and $V_{rms}={\tfrac {V_{0}}{\sqrt {2}}}$ ▭ Impedance $V_{0}=I_{0}X$

▭ Resistor $V_{0}=I_{0}X_{R},\;\phi =0,$ where $X_{R}=R$
▭ Capacitor $V_{0}=I_{0}X_{C},\;\phi =-{\tfrac {\pi }{2}},$ where $X_{C}={\tfrac {1}{\omega C}}$ ▭ Inductor $V_{0}=I_{0}X_{L},\;\phi =+{\tfrac {\pi }{2}},$ where $X_{L}=\omega L$
▭ RLC series circuit $V_{0}=I_{0}Z$ where $Z={\sqrt {R^{2}+\left(X_{L}-X_{C}\right)^{2}}}$ and $\phi =\tan ^{-1}{\frac {X_{L}-X_{C}}{R}}$
▭ Resonant angular frequency $\omega _{0}={\sqrt {\tfrac {1}{LC}}}$ ▭ Quality factor $Q={\tfrac {\omega _{0}}{\Delta \omega }}={\tfrac {\omega _{0}L}{R}}$
▭ Average power $P_{ave}={\frac {1}{2}}I_{0}V_{0}\cos \phi =I_{rms}V_{rms}\cos \phi$, where $\phi =0$ for a resistor.
▭ Transformer voltages and currents ${\tfrac {V_{S}}{V_{P}}}={\tfrac {N_{S}}{N_{P}}}={\tfrac {I_{P}}{I_{S}}}$

Electromagnetic Waves

Displacement current $I_{d}=\varepsilon _{0}{\tfrac {d\Phi _{E}}{dt}}$ where $\Phi _{E}=\int {\vec {E}}\cdot d{\vec {A}}$ is the electric flux.

Maxwell's equations ${\begin{aligned}\oint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {A}}&={\frac {1}{\epsilon _{0}}}Q_{in}\qquad &\oint _{S}{\vec {B}}\cdot \mathrm {d} {\vec {A}}&=0\\\oint _{C}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}&=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot \mathrm {d} {\vec {A}}\qquad &\oint _{C}{\vec {B}}\cdot \mathrm {d} {\vec {\ell }}&=\mu _{0}I+\epsilon _{0}\mu _{0}{\frac {\mathrm {d} \Phi _{E}}{\mathrm {d} t}}\end{aligned}}$
See also http://ethw.org/w/index.php?title=Maxwell%27s_Equations&oldid=157445
▭ Plane EM wave equation ${\frac {\partial ^{2}E_{y}}{\partial x^{2}}}=\varepsilon _{0}\mu _{0}{\frac {\partial ^{2}E_{y}}{\partial t^{2}}}$ where $c={\tfrac {1}{\sqrt {\varepsilon _{0}\mu }}}$ is the speed of light
▭ The ratio of peak electric to magnetic field is ${\tfrac {E_{0}}{B_{0}}}=c$ and the Poynting vector ${\vec {S}}={\tfrac {1}{\mu _{0}}}{\vec {E}}\times {\vec {B}}$ represents the energy flux
▭ Average intensity $I=S_{ave}={\tfrac {c\varepsilon _{0}}{2}}E_{0}^{2}={\tfrac {c}{2\mu _{0}}}B_{0}^{2}={\tfrac {1}{2\mu _{0}}}E_{0}B_{0}$
▭ Radiation pressure $p=I/c$ (perfect absorber) and $p=2I/c$ (perfect reflector).