Portal:Radiation astronomy/Problems

edit  

Selected problems

Angular momentum and energy

Main article: Angular momentum and energy

This diagram describes the relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. 'r' is the radius. Credit: Yawe.

Angular momentum and energy are concepts developed to try to understand everyday reality.

An angular momentum L of a particle about an origin is given by

$\mathbf {L} =\mathbf {r} \times \mathbf {p}$

where r is the radius vector of the particle relative to the origin, p is the linear momentum of the particle, and × denotes the cross product (r · p sin θ). Theta is the angle between r and p.

Please put any questions you may have, and your results, you'd like evaluated, on the problem set's discussion page.

Enjoy learning by doing!

---

Column densities

Main article: Column densities

A region of the sky called the "Lockman Hole", located in the constellation of Ursa Major, is one of the areas surveyed in infrared light by the Herschel Space Observatory. Credit: ESA/Herschel/SPIRE/HerMES.

A column density is the number of units of matter observed along a line of sight that has an area of observation. This area has a height that is the distance to an object, or through which observation is taking place.

"A region of the sky [at right] called the "Lockman Hole", located in the constellation of Ursa Major, is one of the areas surveyed in infrared light by the Herschel Space Observatory. All of the little dots in this picture are distant galaxies. The pattern of their collective light is what's known as the cosmic infrared background. By studying this pattern, astronomers were able to measure how much dark matter it takes to create a galaxy bursting with young stars."

References

---

Cosmic circuits

Main article: Cosmic circuits

The arcing, graceful structure is actually a bow shock about half a light-year across, created from the wind from the star L.L. Orionis colliding with the Orion Nebula flow. Credit: NASA.

This diagram suggests a simple electrical circuit. Credit: GorillaWarfare.

Voyager 1 has found only electrons streaming into the heliosphere from elsewhere in the galaxy. This problem set poses several problems to calculate the possibility that a simple electrical circuit is involved.

The diagram at right suggests a simple electrical circuit.

Def. an enclosed path of an electric current is called a circuit.

In the diagram at right are three components:

1. a voltage (V), or current (i), source,
2. an enclosed path, and
3. a resistance, or resistor, (R).

According to Ohm's law:

$V=iR.$

With respect to an enclosed path, consider a path from outside the heliosphere, inward toward the Sun, and out again. Let the incoming electrons have 500 MeV of energy and a flux of 8.5 x 10⁴ e^- cm^-2 s^-1.

Def. a time rate of flow of electric charge is called a current.

Def. that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to 2 x 10^–7 newton per metre of length is called an ampere.

Def. an amount of electrostatic potential between two points in space is called a voltage.

---

Energy phantoms

Main article: Energy phantoms

This is an optical image in the visual range of Theta Ursae Majoris. It is listed in SIMBAD as an F7V spectral type star with a parallax of 74.19 mas. Credit: Aladin at SIMBAD.

Students start from specific situations of motion, determine how to calculate energy and convert units, then evaluate types of energy.

Def. a quantity that denotes the ability to do work and is measured in a unit dimensioned in mass × distance²/time² (ML²/T²) or the equivalent is called energy.

Def. a physical quantity that denotes ability to push, pull, twist or accelerate a body which is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn) is called force.

In astronomy we estimate distances and times when and where possible to obtain forces and energy.

The key values to determine in both force and energy are (L/T²) and (L²/T²). Force (F) x distance (L) = energy (E), L/T² x L = L²/T². Force and energy are related to distance and time using proportionality constants.

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
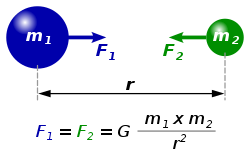
$F=G{\frac {m_{1}m_{2}}{r^{2}}}\$, where: F is the force between the masses, G is the gravitational constant, m1 is the first mass, m2 is the second mass, and r is the distance between the centers of the masses.	The diagram shows two masses attracting one another. Credit: Dna-Dennis.

In the International System of Units (SI) units, F is measured in newtons (N), m₁ and m₂ in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10⁻¹¹
 N m² kg⁻².

Observationally, we may not know the origin of the force.

Coulomb's law states that the electrostatic force $F$ experienced by a charge, $q$ at position $r_{q}$, in the vicinity of another charge, $Q$ at position $r_{Q}$, in vacuum is equal to:

$F={qQ \over 4\pi \varepsilon _{0}}{1 \over {r^{2}}},$

where $\varepsilon _{0}$ is the electric constant and $r$ is the distance between the two charges.

Coulomb's constant is

$k_{e}=1/(4\pi \varepsilon _{0}\varepsilon ),$

where the constant $\varepsilon _{0}$ is called the permittivity of free space in SI units of C² m⁻² N⁻¹.

For reality, $\varepsilon$ is the relative (dimensionless) permittivity of the substance in which the charges may exist.

The energy $E$ for this system is

$E=F\cdot D,$

where $D$ is the displacement.

References

---

Furlongs per fortnight

Main article: Furlongs per fortnight

It's about the chains. Credit: Stilfehler.{{free media}}

Furlongs per fortnight is a problem set with a contained quiz that focuses on the fundamentals of observational and deductive astronomy. In the activity Energy phantoms you learned about the value of distance, or displacement, and motion, speed, velocity, and acceleration. Here, you can practice and test yourself on converting from units that may or have occurred in the literature to units popular today.

Notation: let the symbol $R_{\oplus }$ indicate the Earth's radius.

Notation: let the symbol $R_{J}$ indicate the radius of Jupiter.

Notation: let the symbol $R_{\odot }$ indicate the solar radius.

Both physics and astronomy use units and dimensions to describe observations.

Units of Physics and Astronomy

Dimension	Astronomy	Symbol	Physics	Symbol	Conversion
time	1 day	d	1 second	s	1 d = 86,400 s
time	1 "Julian year"	J	1 second	s	1 J = 31,557,600 s
distance	1 astronomical unit	AU	1 meter	m	1 AU = 149,597,870.691 km
angular distance	1 parsec	pc	1 meter	m	1 pc ~ 30.857 x 1012 km

References

---

Planck's equation

Main article: Planck's equation

Planck's equation (colored curves) accurately describes black body radiation. Credit: Darth Kule.

Planck's equation describes the amount of spectral radiance at a certain wavelength radiated by a black body in thermal equilibrium.

In terms of wavelength (λ), Planck's equation is written as

$B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}$

where B is the spectral radiance, T is the absolute temperature of the black body, k_B is the Boltzmann constant, h is the Planck constant, and c is the speed of light.

This form of the equation contains several constants that are usually not subject to variation with wavelength. These are h, c, and k_B. They may be represented by simple coefficients: c1 = 2h c² and c2 = h c/k_B.

By setting the first partial derivative of Planck's equation in wavelength form equal to zero, iterative calculations may be used to find pairs of (λ,T) that to some significant digits represent the peak wavelength for a given temperature and vice versa.

${\frac {\partial B}{\partial \lambda }}={\frac {c1}{\lambda ^{6}}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}[{\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}-5]=0.$

Or,

${\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}-5=0.$

${\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}=5.$

Use c2 = 1.438833 cm K.

---

Radiation astronomy problem set

Main articles: Radiation astronomy/Problem set and Radiation astronomy problem set

This is a visual image of beta Virginis. Its effective surface temperature is 6,132 K. Credit: Aladin at SIMBAD.

Students start from a specific observational situation, notice changes, and calculate what's happening.

An astronomical radio source is detected on January 3, 2004. Over a period of 10 hours (hrs) of observation the detector records 1,000 counts (cts). The source's position is RA 10^h 10^m 10^s Dec -10° 10' 10". Its distance is 3 AU.

---

Radiation dosages

Main article: Radiation dosage

Cherenkov radiation glows in the core of the Advanced Test Reactor. Credit: Matt Howard.

Various types of radiation including ionizing radiation may cause harm to people, researchers, and students under different situations.

This problem set is designed to help you calculate how much radiation and of what type you may be exposed to and how much damage it might cause.

The idea is forewarned is forearmed so that should you find yourself performing research requiring the use of radiation you will use proper and effective precaution.

Def. any "illness produced by ionizing radiation with symptoms ranging from nausea through to death" is called radiation sickness.

Def. an "addition of a small measured amount of a substance to something" is called a dosage.

Def. a "quantity of an agent (not always active) substance or radiation administered at any one time" is called a dose.

References

---

Radiation astromathematics problem set

Main articles: Radiation astronomy/Mathematics/Problem set and Radiation astromathematics problem set

This composite image shows an exoplanet (2M1207b, the red spot on the lower left), orbiting the brown dwarf 2M1207 (centre). 2M1207b is a Jupiter-like planet. It orbits the brown dwarf at a distance nearly twice as far as Neptune is from the Sun. Credit: ESO.

This radiation mathematics/problem set is a series of mathematical problems that use dimensions.

Notation: let the symbol $R_{\oplus }$ indicate the Earth's radius.

Notation: let the symbol $R_{J}$ indicate the radius of Jupiter.

Notation: let the symbol $R_{\odot }$ indicate the solar radius.

---

Portal:Radiation astronomy/Problems/10

---

Portal:Radiation astronomy/Problems/11

---

Portal:Radiation astronomy/Problems/12

---

Portal:Radiation astronomy/Problems/13

---

Portal:Radiation astronomy/Problems/14

---

Portal:Radiation astronomy/Problems/15

---

Portal:Radiation astronomy/Problems/16

---

Portal:Radiation astronomy/Problems/17

---

Portal:Radiation astronomy/Problems/18

---

Portal:Radiation astronomy/Problems/19

---

Portal:Radiation astronomy/Problems/20

---

Portal:Radiation astronomy/Problems/21

---

Portal:Radiation astronomy/Problems/22

---

Portal:Radiation astronomy/Problems/23

---

Portal:Radiation astronomy/Problems/24

---

Portal:Radiation astronomy/Problems/25

---

Portal:Radiation astronomy/Problems/26

---

Portal:Radiation astronomy/Problems/27

---

Portal:Radiation astronomy/Problems/28

---

Portal:Radiation astronomy/Problems/29

---

Portal:Radiation astronomy/Problems/30

---

Portal:Radiation astronomy/Problems/31

---

Portal:Radiation astronomy/Problems/32

---

Portal:Radiation astronomy/Problems/33

---

Portal:Radiation astronomy/Problems/34

---

Portal:Radiation astronomy/Problems/35

---

Portal:Radiation astronomy/Problems/36

---

Portal:Radiation astronomy/Problems/37

---

Portal:Radiation astronomy/Problems/38

---

Portal:Radiation astronomy/Problems/39

---

Portal:Radiation astronomy/Problems/40

---

Portal:Radiation astronomy/Problems/41

---

Portal:Radiation astronomy/Problems/42

---

Portal:Radiation astronomy/Problems/43

---

Portal:Radiation astronomy/Problems/44

---

Portal:Radiation astronomy/Problems/45

---

Portal:Radiation astronomy/Problems/46

---

Portal:Radiation astronomy/Problems/47

---

Portal:Radiation astronomy/Problems/48

---

Portal:Radiation astronomy/Problems/49

---

Portal:Radiation astronomy/Problems/50

---

Nominating or creating problems

If you have a suggestion for future Selected problems for this portal, please suggest them on the discussion page, or create them yourself. You can also suggest future Selected problems at Portal talk:Radiation astronomy/Problems. If you have any questions, contact User:Marshallsumter or leave a message at Portal Astronomy.