Angular momentum and energy

Angular momentum and energy are concepts developed to try to understand everyday reality.

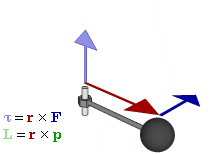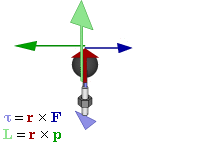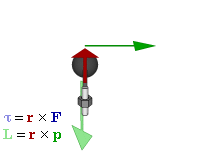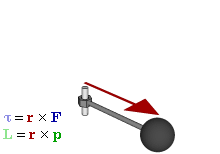
This diagram describes the relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. 'r' is the radius. Credit: Yawe.{{free media}}

An angular momentum L of a particle about an origin is given by

\mathbf {L} =\mathbf {r} \times \mathbf {p}

where r is the radius vector of the particle relative to the origin, p is the linear momentum of the particle, and × denotes the cross product (r · p sin θ). Theta is the angle between r and p.

Masses

Def. the "quantity of matter which a body contains, irrespective of its bulk or volume"^[1] or a "quantity of matter cohering together so as to make one body, or an aggregation of particles or things which collectively make one body or quantity"^[2] is called mass, or a mass.

Mass is an idea.

The smallest unit of mass appears to be an electron (or positron).

Motions

Def. a property of a body that resists any change to its uniform motion is called inertia.

Mass and inertia are generally considered equivalent.

Isaac Newton's laws of motion contain the idea of inertia.

Newton's First law: "Every body persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed."^[3]

While motion in a straight line, or rectilinear motion can be produced over limited distances in a laboratory, it may not occur naturally.

When a body or particle is radiated it is given motion.

Vectors

The angular velocity of the particle at P with respect to the origin O is determined by the perpendicular component of the velocity vector v. Credit: Krishnavedala.{{free media}}

The angular velocity describes the speed of rotation and the orientation of the instantaneous axis about which the rotation occurs. The direction of the angular velocity pseudovector is along the axis of rotation; in this case (counter-clockwise rotation) the vector points up. Credit: dnet.{{free media}}

Def. the product of a body's mass and velocity is called momentum.

Def. the rotary inertia of a system [such as] an isolated rigid body is a measure of the extent to which an object will continue to rotate in the absence of an applied torque is called angular momentum.

Energies

Def. a rotational or twisting effect of a force is called a torque.

Def. a turning effect of a force applied to a rotational system at a distance from the axis of rotation is called a moment of force.

The moment is equal to the magnitude of the force multiplied by the perpendicular distance between its line of action and the axis of rotation.

A torque and a moment of force are the same. Each is a "unit of work done, or energy expended.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

\mathbf {L} =I{\boldsymbol {\omega }}

where I is the moment of inertia of the object (in general, a tensor quantity), and ω is the angular velocity.

The moment of inertia is the mass property of a rigid body that defines the torque needed for a desired angular acceleration about an axis of rotation. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation, of a body about that axis. Moment of inertia depends on the amount and distribution of its mass, and can be found through the sum of moments of inertia of the masses making up the whole object, under the same conditions.

In two dimensions the angular velocity ω is given by

\omega ={\frac {d\phi }{dt}}

This is related to the cross-radial (tangential) velocity by:^[4]

\mathrm {v} _{\perp }=r\,{\frac {d\phi }{dt}}

An explicit formula for v_⊥ in terms of v and θ is:

\mathrm {v} _{\perp }=|\mathrm {\mathbf {v} } |\,\sin(\theta )

"Combining the above equations gives a formula for ω:

\omega ={\frac {|\mathrm {\mathbf {v} } |\sin(\theta )}{|\mathrm {\mathbf {r} } |}}

Problem 1

This is a visual image of the Sun with some sunspots visible on the photosphere. The two small spots in the middle have about the same diameter as our planet Earth. Credit: NASA.{{free media}}

Using the following values, and considering the Sun to be a rigid, solid object, answer the questions below. $R_{\odot eq}=696342km,$ $M_{\odot }=1.9891\times 10^{30}kg,$ and $V_{eqrot}=7.189\times 10^{3}km/h.$

What is the angular velocity of the Sun?

What is its moment of inertia?

What is the Sun's angular momentum?

Estimate how much torque is necessary to bring the Sun's rotational velocity down to zero?

What are the units of angular momentum for the Sun?

Problem 2

This is a composite Cassini–Huygens image of Jupiter. Credit: NASA/JPL/University of Arizona.{{free media}}

Using the following values, and considering Jupiter to be a rigid, solid object, answer the questions below. $R_{Jeq}=71492km,$ $M_{J}=1.8986\times 10^{27}kg,$ and $V_{eqJ}=4.53\times 10^{4}km/h.$

What is the angular velocity of the Jupiter?

What is its moment of inertia?

What is the Jupiter's angular momentum from rotation?

Estimate how much torque is necessary to bring the Jupiter's rotational velocity down to zero?

Using a mean orbital radius between 8.16 x 10⁸ km and 7.41 x 10⁸ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Jupiter greater than the Sun's?

Problem 3

This is an image of Saturn in natural color, photographed by Cassini–Huygens in 2004. Credit: NASA / JPL / Space Science Institute.{{free media}}

Using the following values, and considering Saturn to be a rigid, solid object, answer the questions below. $R_{Seq}=60268km,$ $M_{S}=5.6846\times 10^{24}kg,$ and $V_{eqS}=3.55\times 10^{4}km/h.$

What is the angular velocity of the Saturn?

What is its moment of inertia?

What is the Saturn's angular momentum from rotation?

Estimate how much torque is necessary to bring the Saturn's rotational velocity down to zero?

Using a mean orbital radius between 1.51 x 10⁹ km and 1.35 x 10⁹ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Saturn greater than the Sun's?

Problem 4

This is an image of the planet Uranus taken by the spacecraft Voyager 2 in 1986. Credit: NASA/JPL/Voyager mission.{{free media}}

Using the following values, and considering Uranus to be a rigid, solid object, answer the questions below. $R_{Ueq}=60268km,$ $M_{U}=5.6846\times 10^{24}kg,$ and $V_{eqU}=3.55\times 10^{4}km/h.$

What is the angular velocity of the Uranus?

What is its moment of inertia?

What is the Uranus's angular momentum from rotation?

Estimate how much torque is necessary to bring the Uranus's rotational velocity down to zero?

Using a mean orbital radius between 3.00 x 10⁹ km and 2.75 x 10⁹ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Uranus greater than the Sun's?

Problem 5

This is an image of Neptune from Voyager 2. Credit: NASA/JPL.{{free media}}

Using the following values, and considering Neptune to be a rigid, solid object, answer the questions below. $R_{Neq}=24764km,$ $M_{N}=1.0243\times 10^{26}kg,$ and $V_{eqN}=9.66\times 10^{4}km/h.$

What is the angular velocity of the Neptune?

What is its moment of inertia?

What is the Neptune's angular momentum from rotation?

Estimate how much torque is necessary to bring the Neptune's rotational velocity down to zero?

Using a mean orbital radius between 4.55 x 10¹⁰ km and 4.45 x 10¹⁰ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Neptune greater than the Sun's?

Hypotheses

To use angular momentum or energy a mass must be assigned.

References

↑ Eclecticology (12 September 2003). mass. San Francisco, California: Wikimedia Foundation, Inc. http://en.wiktionary.org/wiki/mass. Retrieved 2013-08-12.
↑ Emperorbma (14 November 2003). mass. San Francisco, California: Wikimedia Foundation, Inc. https://en.wiktionary.org/wiki/mass. Retrieved 2014-02-28.
↑ Isaac Newton, The Principia, A new translation by I.B. Cohen and A. Whitman, University of California press, Berkeley 1999.
↑ Russell C. Hibbeler (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6. http://books.google.com/?id=tOFRjXB-XvMC&pg=PA314.

External links

[MassWikt-1] Eclecticology (12 September 2003). mass. San Francisco, California: Wikimedia Foundation, Inc. http://en.wiktionary.org/wiki/mass. Retrieved 2013-08-12.

[MassWikt1-2] Emperorbma (14 November 2003). mass. San Francisco, California: Wikimedia Foundation, Inc. https://en.wiktionary.org/wiki/mass. Retrieved 2014-02-28.

[Newton-3] Isaac Newton, The Principia, A new translation by I.B. Cohen and A. Whitman, University of California press, Berkeley 1999.

[Hibbeler-4] Russell C. Hibbeler (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6. http://books.google.com/?id=tOFRjXB-XvMC&pg=PA314.

[1]

[2]

[3]

[4]

Angular momentum and energy

Contents

Masses

Motions

Vectors

Energies

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Hypotheses

See also

References

External links