Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I/Lecture 16
- Derivative of power series
Many important functions, like the exponential function or the trigonometric functions, are represented by a power series. The following theorem shows that these functions are differentiable, and that the derivative of a power series is itself a power series, given by differentiating the individual terms of the series.
Let
denote a power series which converges on the open interval , and represents there a function . Then the formally differentiated power series
is convergent on . The function is differentiable in every point of the interval, and
Proof
In the formulation of the theorem, we have distinguished between for the power series and for the function, defined by the series, in order to stress the roles they play. This distinction is now not necessary anymore.
This follows immediately from Theorem 16.1 .
By definition, we have
The derivative with respect to equals
due to Theorem 16.3 and the chain rule.
For a real exponential function
the relation
holds, due to Theorem 16.4 . Hence, there is a proportional relationship between the function and its derivative , and is the factor. This is still true if is multiplied with a constant. If we consider as a function depending on time , then describes the growing behavior at that point of time. The equation means that the instantaneous growing rate is always proportional with the magnitude of the function. Such an increasing behavior (or decreasing behavior, if ) occurs in nature for a population, if there is no competition for resources, and if the dying rate is neglectable (the number of mice is then proportional with the number of mice born). A condition of the form
is an example of a differential equation. This is an equation for a function, which expresses a condition for the derivative. A solution for such a differential equation is a differentiable function which fulfills the condition on its derivative. The differential equation just mentioned are fulfilled by the functions
We will study differential equations in the second semester.
As the logarithm is the inverse function of the exponential function, we can apply Theorem 14.9 and get
using Theorem 16.3 .
By definition, we have
The derivative with respect to equals
using Theorem 16.3 , Corollary 16.6 and the chain rule.
Using the quotient rule, Theorem 16.8 , and the circle equation, we get
The derivative of the cotangent function follows in the same way.
- The number
The number is the area and half of the circumference of a circle with radius . But, in order to build a precise definition for this number on this, we would have first to establish measure theory or the theory of the length of curves. Also, the trigonometric functions have an intuitive interpretation at the unit circle, but also this requires the concept of the arc length. An alternative approach is to define the functions sine and cosine by their power series, and then to define the number with the help of them, and establishing finally the relation with the circle.
The cosine function has, within the real interval , exactly one
zero.We consider the cosine series
For , we have . For , one can write
Hence, due to
the intermediate value theorem,
there exists at least one zero in the given interval.
To prove uniqueness, we consider the
derivative
of cosine, which is
due to Theorem 16.8 . Hence, it is enough to show that sine is positive in the interval , because then cosine is strictly decreasing by Theorem 15.7 in the interval and there is only one zero. Now, for , we have

Let denote the unique (according to Lemma 16.10 ) real zero of the cosine function in the interval . Then the number is defined by
- We have and for all .
- We have and for all .
- We have and for all .
- We have , , , , and .
- We have , , , , and .
Due to the circle equation
we have , hence , because of the reasoning in the proof of Lemma 16.10 . From that we deduce, with the help of the addition theorems, the relations between sine and cosine as mentioned in (3), e.g.
Hence it is enough to prove the statements for cosine. All statements follow from the definition of and from (3).
The trigonometric functions sin and cosine are periodic functions with the period length .
- The inverse trigonometric functions
The real sine function induces a bijective, strictly increasing function
and the real cosine function induces a bijective, strictly decreasing function
Proof
The real tangent function induces a bijective, strictly increasing function
and the real cotangent function induces a bijective strictly decreasing function
Proof
Due to the bijectivity of sine, cosine, tangent and cotangent on suitable interval, there exist the following inverse functions.

The inverse function of the real sine function is

The inverse function of the real cosine function is
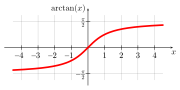
The inverse function of the real tangent function is

The inverse function of the real cotangent function is
The inverse trigonometric functions have the following
derivatives.For example, for the arctangent, we have, due to Theorem 14.9 ,
| << | Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I | >> PDF-version of this lecture Exercise sheet for this lecture (PDF) |
|---|

![{\displaystyle {}]-r,r[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be92ec31de8ca4b998ea7227b7b3b5c363713765)
![{\displaystyle {}f\colon ]-r,r[\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9986ed78b089d43e6e6ca0846ffe3ff3e49d02ca)












































![{\displaystyle {}[0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16a500881b91a2cffe370f70cb70d470f894e184)






![{\displaystyle {}]0,2[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4b5eda7dcd4e7f1ff19cca0efe58996d75e76e)
![{\displaystyle {}x\in {]0,2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87a6aae3d6ff3d676031259a6b2448264371119c)




























![{\displaystyle [-\pi /2,\pi /2]\longrightarrow [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527f8bc31212ec82e3778cde36b1ed32192bf657)
![{\displaystyle [0,\pi ]\longrightarrow [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbd9728b307c63938254cd4e4aff49bc8e2f2a7)
![{\displaystyle ]-\pi /2,\pi /2[\longrightarrow \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54b80848470e2b293193379bd774648a7d69df6)
![{\displaystyle [0,\pi ]\longrightarrow \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/014d0207862d72a4533c62948f6bae80d18e9964)
![{\displaystyle [-1,1]\longrightarrow [-{\frac {\pi }{2}},{\frac {\pi }{2}}],x\longmapsto \arcsin x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e269068b1687b0c1f9ad4b5014b4e7cb54b611)
![{\displaystyle [-1,1]\longrightarrow [0,\pi ],x\longmapsto \arccos x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ecd68470a9279fb3e2ea542385322310d9b0f7f)
![{\displaystyle \mathbb {R} \longrightarrow ]-{\frac {\pi }{2}},{\frac {\pi }{2}}[,x\longmapsto \arctan x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a599a936531a4aaefac1af5be86d23f98e145ce7)
![{\displaystyle \mathbb {R} \longrightarrow ]0,\pi [,x\longmapsto \operatorname {arccot} x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6f643c1b07952f1bae062cf8e79a6d782e9011f)




