Electronics/Resistors

Subject classification: this is a science resource.

Educational level: this is a secondary education resource.

Type classification: this is a lesson resource.

Completion status: this resource is ~75% complete.

This is a lesson in the course Electronics, which is a part of the School:Electronics

A resistor ( $R$ ) is an electronic component that resists, restricts, or opposes the flow of electricalcurrent.

It can be visualized as constriction or narrowing in a pipe, where the constricted area is the resistance (resistor), and the flow of water is current. The volume of water flow following a constriction in a water pipe is reduced.The resistive property of this type of component can be attributed to a material which has much lower electrical conductivity than regular conductive materials such as metals.

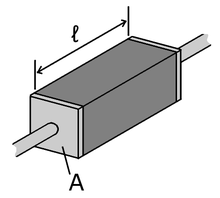
The electrical resistance of a given object depends primarily on two factors:

What material is it made?
what is shape?

therefore, can be computed as:

$R=\rho {\frac {l}{A}}$

where $l$ is the length of the conductor, measured in metres [m], A is the cross-section area of the conductor measured in square metres [m²] and ρ (rho) is the electrical resistivity (also called specific electrical resistance) of the material, measured in ohm-metres (Ω·m).

In This formula $\rho ,{l},{A}$ are constant,therefore $R$ already is constant.

The inverse resistance $R$ is conductance $G$ , the ease at which an electric current passes.therefore, can be computed as:

$G={\frac {1}{R}}={\frac {1}{\rho }}\cdot {\frac {A}{l}}$

${\frac {1}{\rho }}=\sigma$ → $\sigma$ ([[Sigma (sigma) is the electrical conductivity measured in siemens per meter(S·m⁻¹)

$G={\frac {1}{R}}=\sigma \cdot {\frac {A}{l}}$

In This formula $\sigma ,{A},{l},$ are constant,therefore $G$ already is constant.

V, I, and R, the parameters of Ohm's law.

Electrical current ( $I$ ) results when a voltage ( $V$ ) (or electromagnetic force) causes movement of electrons.

Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points.

I\propto V

then: ↑

V

→ ↑

I

and ↓

V

→ ↓

I

In the electric circuit, if temperature and all other conditions remain constant, R and G are constant therefore relationship between I and V is linearity then:

I=G\cdot V\;\;\;\;\;\;\;and\;\;\;\;\;\;\;G={\frac {1}{R}}

I={\frac {1}{R}}\cdot V\;\;\;\;\;\;\;or\;\;\;\;\;\;\;I={\frac {V}{R}}

R=1,G=1

R>1,G<1

R<1,G>1

Ohm's law can be used to calculate the resistance present in a DC circuit if voltage and current are known.

Resistance

Every resistor has a resistance calculated as:

I={\frac {V}{R}}

→

R={\frac {V}{I}}

where:

R is resistance (ohms, Ω),

V is voltage (volts, V),

I is current (amperes, A).

Conductance

Conductance (G) is defined as the inverse of resistance, calculated as:

$G={\frac {1}{R}}$

where:

G is conductance (siemens, S).

Voltage

Voltage is calculated as:

I={\frac {V}{R}}

→

V=I\cdot R

Current

Current is calculated as:

$I={\frac {V}{R}}$

Power

Power is calculated as:

P=I\cdot V\;\;\;\;\;\;\ and\;\;\;\;\;\;\ I={\frac {V}{R}}\;\;\;\;\;\;\ and\;\;\;\;\;\;\ V=R\cdot I

P=I^{2}R\;\;\;\;\;\;\ P={\frac {V^{2}}{R}}

Resistor color code

Color	Significant figures	Multiplier	Tolerance		Temp. Coefficient (ppm/K)
Black	0	×10⁰	–		250	U
Brown	1	×10¹	±1%	F	100	S
Red	2	×10²	±2%	G	50	R
Orange	3	×10³	–		15	P
Yellow	4	×10⁴	(±5%)	–	25	Q
Green	5	×10⁵	±0.5%	D	20	Z
Blue	6	×10⁶	±0.25%	C	10	Z
Violet	7	×10⁷	±0.1%	B	5	M
Gray	8	×10⁸	±0.05% (±10%)	A	1	K
White	9	×10⁹	–		–
Gold	–	×10^-1	±5%	J	–
Silver	–	×10^-2	±10%	K	–
None	–	–	±20%	M	–

Any temperature coefficent not assigned its own letter shall be marked "Z", and the coefficient found in other documentation. For more information, see EN 60062. Yellow and Gray are used in high-voltage resistors to avoid metal particles in the lacquer.

Resistors found in electronic kits and hobby projects have up to four bars indicating the color code. The first two bars represent the first and second significant digit, the third represents the exponent or decimal multiplier, and the fourth represents the tolerance. The chart to the right shows information about the color coding on resistors.

External Links

Wikipedia: Resistor