Electric Circuit Analysis/Resistors in Parallel
 
|
Lesson 3: ReviewWhat you need to remember from Resistors in Series. If you ever feel lost, do not shy away from going back to the previous lesson & going through it again. You can learn by repetition.
Lesson 4: PreviewThis Lesson is about Resistors in Parallel. The student/user is expected to understand the following at the end of the lesson.
|
| ||||||||||||||||||||||||||||||||||||||||||||||
Part 1IntroductionThe best way to understand Parallel circuits is to start with the definition. A circuit is parallel to another circuit or several circuits if and only if they share common terminals; i.e. if both the branches touch each other's endpoints. Here is an example:
Something interesting happens as the current reaches the common node of resistors that are connected in parallel: the total current is divided into the parallel branches.
|
Part 2Voltage RuleIf two or more branches are parallel then the voltage across them is equal. So based on this we can conclude that . However, unlike series resistors, the current across the branches is not necessarily equal. Equivalent resistanceFor series resistors to find the total resistance we simply add them together. For parallel resistors, it's a little more complicated. Instead, we use the following equation: However, for the case of only two resistors, we can use the following simplified form: Equation 4.2: Total Parallel Resistance It is well to note at this point that the total resistance of parallel-connected resistors will always be less than the resistance of the smallest of the individual resistors. Current RuleIn series connection, we deduced that voltage is divided amongst resistors. For parallel-connected resistors, however, the current is divided. So, as we did with the voltage division principle, here is the mathematical formula: Equation 4.3: Current Divider Formula
Using this formula you can work out the currents flowing through individual resistors. |
Part 3ApplicationWe have spent three lectures hacking on about what and why resistors and resistive circuits in two connection schemes are used (i.e. series and parallel connections). The question now is, where and how in real life do these connections happen?
One simple application of these connection schemes is the Shunt Application. In the electric measurement industry, most often enough, we wish to measure currents and voltages of very high magnitudes (in the range of 500kV upwards). The problem is that metering devices have delicate electronic components and usually have small voltage and current ratings.
The solution to the above problem is to have a metering device connected in parallel to a resistor, with the resistor thus called a "shunt" resistor since it is there to protect (shunt) the metering device as shown in Part 4. |
Part 4If we know the current rating of a device and the total current in the system, we can then work out the shunt current and, thus, the shunt resistance. |
Part 5: Examples
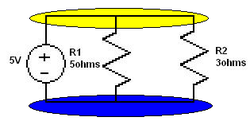
Figure 3.4 shows a parallel resistive circuit with the following parameters.
Find , and Solution: from Equation 4.2 we see that.
Thus it can be said that the supply current has been divided between R1 and R2.
We know that when solving these problems, we look at the data given and thus we can see how we need to manipulate our equations in order to achieve our objective.The following example highlights this point. See to it that you follow the method used and the reasoning behind it. |
Part 6: Examples
Figure 4.5 shows a parallel resistive circuit with the following parameters.
Find: and Solution: from Equation 3.2 we see that.
| ||||||||||||
Part 7Do you Remember?Let's take some time to Reflect on the Material covered thus far. We have learned a great deal about simple resistive circuits and the possible connections they afford us. Here I think you'll want to remember:
Do Exercise 4 in Part 8. After being completely satisfied with your work, you can go on to the next page - for the quiz! Good luck :-) Related Topic(s) in WikiversityPlease visit the following page to supplement material covered in this lesson
|
Part 8: Exercise 4
 Completion listOnce you finish your Exercises you can post your score here!
To post your score just e-mail your course coordinator your name and score *Click Here
|
| Resource type: this resource contains a lecture or lecture notes. |
External Links
- Resistors Series and Parallel: Electronics for Beginners
´