4-ary Boolean functions
| Studies of Boolean functions |
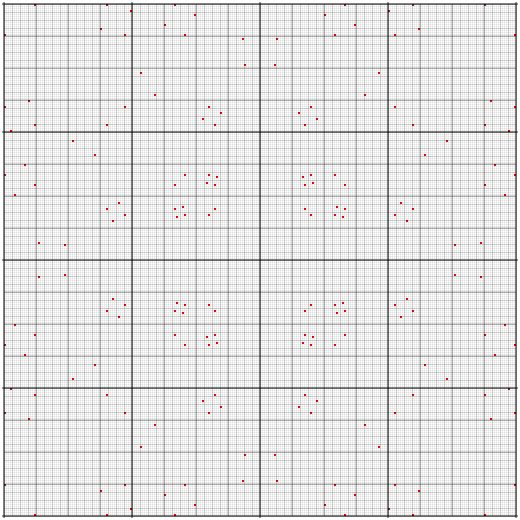
There are = 65536 4-ary Boolean functions, which correspond to 16-bit binary strings.

0000 0001 0001 0110
Big equivalence classes (bec)
editWhen binarily colored tesseracts can be transformed into each other by actions in the tesseract's symmetry group C4, they are essentially the same.
The corresponding Boolean functions are often called equivalent and belong to the same big equivalence class (bec).
The 65536 functions belong to 1 + 1 + 4 + 6 + 19 + 27 + 50 + 56 + 74 + 56 + 50 + 27 + 19 + 6 + 4 + 1 + 1 = 402 becs.
The following sortable table (in the collapsed box) shows the 402 becs with some key features.
The default order is that of the numbers in column N. Sorting by # sorts also by N.
The numbers in column weight are the hamming weights of the functions, i.e. the number of ones in the binary strings.
Column sec tells the number of secs in the bec. Column f tells the number of functions in the bec.
The function with the smallest numerical value is shown in column F as an example. It's numerical value is shown in column N.
becs with an entry in column sona are related to subgroups of nimber addition.
The entry in column wec denotes the Walsh equivalence class the bec belongs to.
The nonlinearity of all functions in the bec is shown in column nonlin.
Functions with nonlinearity 0 are linear, those with nonlinearity 6 are bent.
To sort by more than one column you can hold the shift-key and than click the other sort buttons. *
Greatest big equivalence classes (ggbec)
edit| Table of the 39 ggbecs | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Walsh equivalence classes (wec)
edit| 32768 = 215 |
|
| 2048 = 211 |
| ||
| 8192 = 213 |
| ||
| 12288 = 212 * 3 |
| ||
| 8192 = 213 |
| ||
| 2048 = 211 |
|
| wec E0 and wec E4 |
|---|
 |
| wec E1 and wec E3 |
|---|
 |
Ring count vectors (rcv)
editA step back:
The 16 2-ary Boolean functions correspond to the subsets of the nested set or hereditarily finite set V3 = P3({}) = { {} , {{}} , {{{}}} , {{},{{}}} }.
That is hard to read, so the nested sets are represented by nested rings of different size.
In the same way every 4-ary Boolean function corresponds to a subset of V4 = P4({}):
| 1111 1111 1111 1111 |
|---|
This set corresponds to the tautology. The cardinality of the subsets of V4 corresponds to the weight of the functions, in this case 16. Without the outer ring there are four different sizes of rings in these graphics. By counting also the smaller rings, the concept of weight can be refined, which leads to a 4-place ring count vector (rcv) for every 4-ary Boolean function. For the tautology it is (16,32,32,16).
For the next function the rcv is (8,16,16,8):
| 1001 1001 0011 1100 |
|---|
The vectors are not always so regular. For the next function it is (7,10,8,4):
| 1111 0110 0000 1000 |
|---|
Every set of 4-ary Boolean functions has a 5-place rcv where the first digit is the set's cardinality. E.g. the set that contains only the above-mentioned function has the rcv (1,7,10,8,4).
Sets of functions that are of some interest are equivalence classes. The last four digits in the rcvs of equivalence classes usually have the pattern n,2n,2n,n.
In the ggbec table above only the first digits are shown, because the rcvs have the pattern n,8n,16n,16n,8n. This is also true for the wec table, because a wec is a union of many ggbecs.
Every rcv has a leading one for the surrounding set, but for the sake of brevity it was omitted here. With it the sums are ![]() A116549.
A116549.
Hamming weight 8
editThere are = 12870 balanced 4-ary Boolean functions (with 8 ones in their binary string).
They belong to 74 becs, which are linked in the following table:
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|
|
0T |
04 |
||||||
|
0T |
|||||||
|
03812 | |||||||
|
0S4 |
0S4 |
041 |
|||||
|
02811 | |||||||
|
01S34 |
03S14 |
04013 | |||||
|
04022 | |||||||
|
0 11 22 33 4 0 11 2222 33 | |||||||
|
0 111 222 3 S 1 222 333 4 |
0 1 222 333 S 111 222 3 4 | ||||||
|
0 222222 4 0 1111 3333 |
The numbers 0, 4, 8, T (twelve) and S (sixteen) tell the number of dots in the last line of the small matrices.
The subscripts on the left side tell the rank of the lines without dots in the small matrices.
(The top row with rank 0 is always without dots, so the 0 is always there.)
The subscripts on the right side tell the rank of the lines full of dots.
The rank of a line is the number of negated arguments.
(Compare big matrices, where the arguments are shown. The top line of a matrix has rank 0, the last line has rank 4.)
The dots in the big matrices show the bits that differ from the top line in the whole bec (the whole file).
The dots in the small matrices show the bits that differ from the top line in the sec (the actual matrix).
Big equivalence classes that are complements (and thus form a gbecs) are linked next to each other.
Links are bold when the bec contains self complementary secs with 16 elements.
Subgroups of nimber addition
editBent functions
editThere are 896 4-ary Bent functions,
which belong to four different greater big equivalence classes (gbecs).
Their nonlinearity is and their Hamming weight is .
Only the functions with Hamming weight 6 are shown. Those with Hamming weight 10 are their complements.
 with 16 functions. |
 of a 4-ary bent function: Belongs to BEC 381 with 3*16 functions. |
 with 12*16 functions. |
 with 12*16 functions. |
| Big equivalence classes (becs) | |||||||
|---|---|---|---|---|---|---|---|
(16 + 48 + 192 + 192) * 2 = 896 |
It's worth taking a look at the distribution of dots in the small matrices in the bec files.
They are all closely related to permuted Walsh matrices,
which is not the case for any other 4-ary Boolean functions.
Even more: Only the bent functions have 8 dots in every row (except the top row) of the small matrices.
![]() Walsh permutation; bent functions
Walsh permutation; bent functions
About the bec files
editThe files in this category describe big equivalence classes (becs).
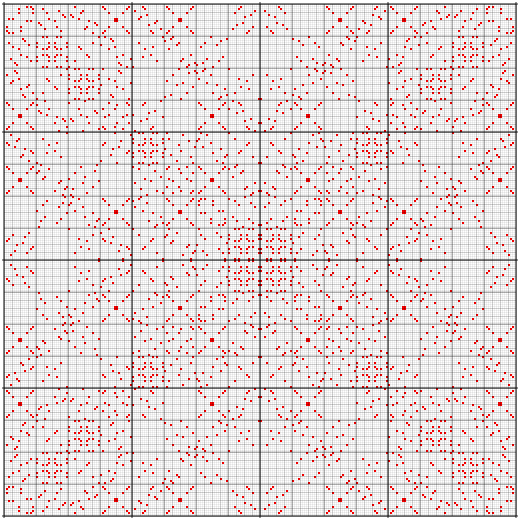
They contain 24 sections, showing 16×16 sec matrices and a number between 0 and 23, representing a permutation of the four arguments.
The big matrices and the small matrices on the right show the same background colors representing binary numbers, but they differ in the dots.
In the big matrices the dots show which fields differ from the top row in the top matrix, while in the small matrices the dots show which fields differ from the top row of the matrix itself.
The numbers in the small left matrices show how the bits of the Boolean function in the top row of the top matrix are permuted.
Their top rows are bit permutations.
| The 24 small left matrices |
|---|
|
M00 = 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14
2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13
3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12
4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11
5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10
6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9
7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8
8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7
9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6
10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5
11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4
12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3
13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2
14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
M01 = 0 2 1 3 4 6 5 7 8 10 9 11 12 14 13 15
2 0 3 1 6 4 7 5 10 8 11 9 14 12 15 13
1 3 0 2 5 7 4 6 9 11 8 10 13 15 12 14
3 1 2 0 7 5 6 4 11 9 10 8 15 13 14 12
4 6 5 7 0 2 1 3 12 14 13 15 8 10 9 11
6 4 7 5 2 0 3 1 14 12 15 13 10 8 11 9
5 7 4 6 1 3 0 2 13 15 12 14 9 11 8 10
7 5 6 4 3 1 2 0 15 13 14 12 11 9 10 8
8 10 9 11 12 14 13 15 0 2 1 3 4 6 5 7
10 8 11 9 14 12 15 13 2 0 3 1 6 4 7 5
9 11 8 10 13 15 12 14 1 3 0 2 5 7 4 6
11 9 10 8 15 13 14 12 3 1 2 0 7 5 6 4
12 14 13 15 8 10 9 11 4 6 5 7 0 2 1 3
14 12 15 13 10 8 11 9 6 4 7 5 2 0 3 1
13 15 12 14 9 11 8 10 5 7 4 6 1 3 0 2
15 13 14 12 11 9 10 8 7 5 6 4 3 1 2 0
M02 = 0 1 4 5 2 3 6 7 8 9 12 13 10 11 14 15
1 0 5 4 3 2 7 6 9 8 13 12 11 10 15 14
4 5 0 1 6 7 2 3 12 13 8 9 14 15 10 11
5 4 1 0 7 6 3 2 13 12 9 8 15 14 11 10
2 3 6 7 0 1 4 5 10 11 14 15 8 9 12 13
3 2 7 6 1 0 5 4 11 10 15 14 9 8 13 12
6 7 2 3 4 5 0 1 14 15 10 11 12 13 8 9
7 6 3 2 5 4 1 0 15 14 11 10 13 12 9 8
8 9 12 13 10 11 14 15 0 1 4 5 2 3 6 7
9 8 13 12 11 10 15 14 1 0 5 4 3 2 7 6
12 13 8 9 14 15 10 11 4 5 0 1 6 7 2 3
13 12 9 8 15 14 11 10 5 4 1 0 7 6 3 2
10 11 14 15 8 9 12 13 2 3 6 7 0 1 4 5
11 10 15 14 9 8 13 12 3 2 7 6 1 0 5 4
14 15 10 11 12 13 8 9 6 7 2 3 4 5 0 1
15 14 11 10 13 12 9 8 7 6 3 2 5 4 1 0
M03 = 0 2 4 6 1 3 5 7 8 10 12 14 9 11 13 15
2 0 6 4 3 1 7 5 10 8 14 12 11 9 15 13
4 6 0 2 5 7 1 3 12 14 8 10 13 15 9 11
6 4 2 0 7 5 3 1 14 12 10 8 15 13 11 9
1 3 5 7 0 2 4 6 9 11 13 15 8 10 12 14
3 1 7 5 2 0 6 4 11 9 15 13 10 8 14 12
5 7 1 3 4 6 0 2 13 15 9 11 12 14 8 10
7 5 3 1 6 4 2 0 15 13 11 9 14 12 10 8
8 10 12 14 9 11 13 15 0 2 4 6 1 3 5 7
10 8 14 12 11 9 15 13 2 0 6 4 3 1 7 5
12 14 8 10 13 15 9 11 4 6 0 2 5 7 1 3
14 12 10 8 15 13 11 9 6 4 2 0 7 5 3 1
9 11 13 15 8 10 12 14 1 3 5 7 0 2 4 6
11 9 15 13 10 8 14 12 3 1 7 5 2 0 6 4
13 15 9 11 12 14 8 10 5 7 1 3 4 6 0 2
15 13 11 9 14 12 10 8 7 5 3 1 6 4 2 0
M04 = 0 4 1 5 2 6 3 7 8 12 9 13 10 14 11 15
4 0 5 1 6 2 7 3 12 8 13 9 14 10 15 11
1 5 0 4 3 7 2 6 9 13 8 12 11 15 10 14
5 1 4 0 7 3 6 2 13 9 12 8 15 11 14 10
2 6 3 7 0 4 1 5 10 14 11 15 8 12 9 13
6 2 7 3 4 0 5 1 14 10 15 11 12 8 13 9
3 7 2 6 1 5 0 4 11 15 10 14 9 13 8 12
7 3 6 2 5 1 4 0 15 11 14 10 13 9 12 8
8 12 9 13 10 14 11 15 0 4 1 5 2 6 3 7
12 8 13 9 14 10 15 11 4 0 5 1 6 2 7 3
9 13 8 12 11 15 10 14 1 5 0 4 3 7 2 6
13 9 12 8 15 11 14 10 5 1 4 0 7 3 6 2
10 14 11 15 8 12 9 13 2 6 3 7 0 4 1 5
14 10 15 11 12 8 13 9 6 2 7 3 4 0 5 1
11 15 10 14 9 13 8 12 3 7 2 6 1 5 0 4
15 11 14 10 13 9 12 8 7 3 6 2 5 1 4 0
M05 = 0 4 2 6 1 5 3 7 8 12 10 14 9 13 11 15
4 0 6 2 5 1 7 3 12 8 14 10 13 9 15 11
2 6 0 4 3 7 1 5 10 14 8 12 11 15 9 13
6 2 4 0 7 3 5 1 14 10 12 8 15 11 13 9
1 5 3 7 0 4 2 6 9 13 11 15 8 12 10 14
5 1 7 3 4 0 6 2 13 9 15 11 12 8 14 10
3 7 1 5 2 6 0 4 11 15 9 13 10 14 8 12
7 3 5 1 6 2 4 0 15 11 13 9 14 10 12 8
8 12 10 14 9 13 11 15 0 4 2 6 1 5 3 7
12 8 14 10 13 9 15 11 4 0 6 2 5 1 7 3
10 14 8 12 11 15 9 13 2 6 0 4 3 7 1 5
14 10 12 8 15 11 13 9 6 2 4 0 7 3 5 1
9 13 11 15 8 12 10 14 1 5 3 7 0 4 2 6
13 9 15 11 12 8 14 10 5 1 7 3 4 0 6 2
11 15 9 13 10 14 8 12 3 7 1 5 2 6 0 4
15 11 13 9 14 10 12 8 7 3 5 1 6 2 4 0
M06 = 0 1 2 3 8 9 10 11 4 5 6 7 12 13 14 15
1 0 3 2 9 8 11 10 5 4 7 6 13 12 15 14
2 3 0 1 10 11 8 9 6 7 4 5 14 15 12 13
3 2 1 0 11 10 9 8 7 6 5 4 15 14 13 12
8 9 10 11 0 1 2 3 12 13 14 15 4 5 6 7
9 8 11 10 1 0 3 2 13 12 15 14 5 4 7 6
10 11 8 9 2 3 0 1 14 15 12 13 6 7 4 5
11 10 9 8 3 2 1 0 15 14 13 12 7 6 5 4
4 5 6 7 12 13 14 15 0 1 2 3 8 9 10 11
5 4 7 6 13 12 15 14 1 0 3 2 9 8 11 10
6 7 4 5 14 15 12 13 2 3 0 1 10 11 8 9
7 6 5 4 15 14 13 12 3 2 1 0 11 10 9 8
12 13 14 15 4 5 6 7 8 9 10 11 0 1 2 3
13 12 15 14 5 4 7 6 9 8 11 10 1 0 3 2
14 15 12 13 6 7 4 5 10 11 8 9 2 3 0 1
15 14 13 12 7 6 5 4 11 10 9 8 3 2 1 0
M07 = 0 2 1 3 8 10 9 11 4 6 5 7 12 14 13 15
2 0 3 1 10 8 11 9 6 4 7 5 14 12 15 13
1 3 0 2 9 11 8 10 5 7 4 6 13 15 12 14
3 1 2 0 11 9 10 8 7 5 6 4 15 13 14 12
8 10 9 11 0 2 1 3 12 14 13 15 4 6 5 7
10 8 11 9 2 0 3 1 14 12 15 13 6 4 7 5
9 11 8 10 1 3 0 2 13 15 12 14 5 7 4 6
11 9 10 8 3 1 2 0 15 13 14 12 7 5 6 4
4 6 5 7 12 14 13 15 0 2 1 3 8 10 9 11
6 4 7 5 14 12 15 13 2 0 3 1 10 8 11 9
5 7 4 6 13 15 12 14 1 3 0 2 9 11 8 10
7 5 6 4 15 13 14 12 3 1 2 0 11 9 10 8
12 14 13 15 4 6 5 7 8 10 9 11 0 2 1 3
14 12 15 13 6 4 7 5 10 8 11 9 2 0 3 1
13 15 12 14 5 7 4 6 9 11 8 10 1 3 0 2
15 13 14 12 7 5 6 4 11 9 10 8 3 1 2 0
M08 = 0 1 4 5 8 9 12 13 2 3 6 7 10 11 14 15
1 0 5 4 9 8 13 12 3 2 7 6 11 10 15 14
4 5 0 1 12 13 8 9 6 7 2 3 14 15 10 11
5 4 1 0 13 12 9 8 7 6 3 2 15 14 11 10
8 9 12 13 0 1 4 5 10 11 14 15 2 3 6 7
9 8 13 12 1 0 5 4 11 10 15 14 3 2 7 6
12 13 8 9 4 5 0 1 14 15 10 11 6 7 2 3
13 12 9 8 5 4 1 0 15 14 11 10 7 6 3 2
2 3 6 7 10 11 14 15 0 1 4 5 8 9 12 13
3 2 7 6 11 10 15 14 1 0 5 4 9 8 13 12
6 7 2 3 14 15 10 11 4 5 0 1 12 13 8 9
7 6 3 2 15 14 11 10 5 4 1 0 13 12 9 8
10 11 14 15 2 3 6 7 8 9 12 13 0 1 4 5
11 10 15 14 3 2 7 6 9 8 13 12 1 0 5 4
14 15 10 11 6 7 2 3 12 13 8 9 4 5 0 1
15 14 11 10 7 6 3 2 13 12 9 8 5 4 1 0
M09 = 0 2 4 6 8 10 12 14 1 3 5 7 9 11 13 15
2 0 6 4 10 8 14 12 3 1 7 5 11 9 15 13
4 6 0 2 12 14 8 10 5 7 1 3 13 15 9 11
6 4 2 0 14 12 10 8 7 5 3 1 15 13 11 9
8 10 12 14 0 2 4 6 9 11 13 15 1 3 5 7
10 8 14 12 2 0 6 4 11 9 15 13 3 1 7 5
12 14 8 10 4 6 0 2 13 15 9 11 5 7 1 3
14 12 10 8 6 4 2 0 15 13 11 9 7 5 3 1
1 3 5 7 9 11 13 15 0 2 4 6 8 10 12 14
3 1 7 5 11 9 15 13 2 0 6 4 10 8 14 12
5 7 1 3 13 15 9 11 4 6 0 2 12 14 8 10
7 5 3 1 15 13 11 9 6 4 2 0 14 12 10 8
9 11 13 15 1 3 5 7 8 10 12 14 0 2 4 6
11 9 15 13 3 1 7 5 10 8 14 12 2 0 6 4
13 15 9 11 5 7 1 3 12 14 8 10 4 6 0 2
15 13 11 9 7 5 3 1 14 12 10 8 6 4 2 0
M10 = 0 4 1 5 8 12 9 13 2 6 3 7 10 14 11 15
4 0 5 1 12 8 13 9 6 2 7 3 14 10 15 11
1 5 0 4 9 13 8 12 3 7 2 6 11 15 10 14
5 1 4 0 13 9 12 8 7 3 6 2 15 11 14 10
8 12 9 13 0 4 1 5 10 14 11 15 2 6 3 7
12 8 13 9 4 0 5 1 14 10 15 11 6 2 7 3
9 13 8 12 1 5 0 4 11 15 10 14 3 7 2 6
13 9 12 8 5 1 4 0 15 11 14 10 7 3 6 2
2 6 3 7 10 14 11 15 0 4 1 5 8 12 9 13
6 2 7 3 14 10 15 11 4 0 5 1 12 8 13 9
3 7 2 6 11 15 10 14 1 5 0 4 9 13 8 12
7 3 6 2 15 11 14 10 5 1 4 0 13 9 12 8
10 14 11 15 2 6 3 7 8 12 9 13 0 4 1 5
14 10 15 11 6 2 7 3 12 8 13 9 4 0 5 1
11 15 10 14 3 7 2 6 9 13 8 12 1 5 0 4
15 11 14 10 7 3 6 2 13 9 12 8 5 1 4 0
M11 = 0 4 2 6 8 12 10 14 1 5 3 7 9 13 11 15
4 0 6 2 12 8 14 10 5 1 7 3 13 9 15 11
2 6 0 4 10 14 8 12 3 7 1 5 11 15 9 13
6 2 4 0 14 10 12 8 7 3 5 1 15 11 13 9
8 12 10 14 0 4 2 6 9 13 11 15 1 5 3 7
12 8 14 10 4 0 6 2 13 9 15 11 5 1 7 3
10 14 8 12 2 6 0 4 11 15 9 13 3 7 1 5
14 10 12 8 6 2 4 0 15 11 13 9 7 3 5 1
1 5 3 7 9 13 11 15 0 4 2 6 8 12 10 14
5 1 7 3 13 9 15 11 4 0 6 2 12 8 14 10
3 7 1 5 11 15 9 13 2 6 0 4 10 14 8 12
7 3 5 1 15 11 13 9 6 2 4 0 14 10 12 8
9 13 11 15 1 5 3 7 8 12 10 14 0 4 2 6
13 9 15 11 5 1 7 3 12 8 14 10 4 0 6 2
11 15 9 13 3 7 1 5 10 14 8 12 2 6 0 4
15 11 13 9 7 3 5 1 14 10 12 8 6 2 4 0
M12 = 0 1 8 9 2 3 10 11 4 5 12 13 6 7 14 15
1 0 9 8 3 2 11 10 5 4 13 12 7 6 15 14
8 9 0 1 10 11 2 3 12 13 4 5 14 15 6 7
9 8 1 0 11 10 3 2 13 12 5 4 15 14 7 6
2 3 10 11 0 1 8 9 6 7 14 15 4 5 12 13
3 2 11 10 1 0 9 8 7 6 15 14 5 4 13 12
10 11 2 3 8 9 0 1 14 15 6 7 12 13 4 5
11 10 3 2 9 8 1 0 15 14 7 6 13 12 5 4
4 5 12 13 6 7 14 15 0 1 8 9 2 3 10 11
5 4 13 12 7 6 15 14 1 0 9 8 3 2 11 10
12 13 4 5 14 15 6 7 8 9 0 1 10 11 2 3
13 12 5 4 15 14 7 6 9 8 1 0 11 10 3 2
6 7 14 15 4 5 12 13 2 3 10 11 0 1 8 9
7 6 15 14 5 4 13 12 3 2 11 10 1 0 9 8
14 15 6 7 12 13 4 5 10 11 2 3 8 9 0 1
15 14 7 6 13 12 5 4 11 10 3 2 9 8 1 0
M13 = 0 2 8 10 1 3 9 11 4 6 12 14 5 7 13 15
2 0 10 8 3 1 11 9 6 4 14 12 7 5 15 13
8 10 0 2 9 11 1 3 12 14 4 6 13 15 5 7
10 8 2 0 11 9 3 1 14 12 6 4 15 13 7 5
1 3 9 11 0 2 8 10 5 7 13 15 4 6 12 14
3 1 11 9 2 0 10 8 7 5 15 13 6 4 14 12
9 11 1 3 8 10 0 2 13 15 5 7 12 14 4 6
11 9 3 1 10 8 2 0 15 13 7 5 14 12 6 4
4 6 12 14 5 7 13 15 0 2 8 10 1 3 9 11
6 4 14 12 7 5 15 13 2 0 10 8 3 1 11 9
12 14 4 6 13 15 5 7 8 10 0 2 9 11 1 3
14 12 6 4 15 13 7 5 10 8 2 0 11 9 3 1
5 7 13 15 4 6 12 14 1 3 9 11 0 2 8 10
7 5 15 13 6 4 14 12 3 1 11 9 2 0 10 8
13 15 5 7 12 14 4 6 9 11 1 3 8 10 0 2
15 13 7 5 14 12 6 4 11 9 3 1 10 8 2 0
M14 = 0 1 8 9 4 5 12 13 2 3 10 11 6 7 14 15
1 0 9 8 5 4 13 12 3 2 11 10 7 6 15 14
8 9 0 1 12 13 4 5 10 11 2 3 14 15 6 7
9 8 1 0 13 12 5 4 11 10 3 2 15 14 7 6
4 5 12 13 0 1 8 9 6 7 14 15 2 3 10 11
5 4 13 12 1 0 9 8 7 6 15 14 3 2 11 10
12 13 4 5 8 9 0 1 14 15 6 7 10 11 2 3
13 12 5 4 9 8 1 0 15 14 7 6 11 10 3 2
2 3 10 11 6 7 14 15 0 1 8 9 4 5 12 13
3 2 11 10 7 6 15 14 1 0 9 8 5 4 13 12
10 11 2 3 14 15 6 7 8 9 0 1 12 13 4 5
11 10 3 2 15 14 7 6 9 8 1 0 13 12 5 4
6 7 14 15 2 3 10 11 4 5 12 13 0 1 8 9
7 6 15 14 3 2 11 10 5 4 13 12 1 0 9 8
14 15 6 7 10 11 2 3 12 13 4 5 8 9 0 1
15 14 7 6 11 10 3 2 13 12 5 4 9 8 1 0
M15 = 0 2 8 10 4 6 12 14 1 3 9 11 5 7 13 15
2 0 10 8 6 4 14 12 3 1 11 9 7 5 15 13
8 10 0 2 12 14 4 6 9 11 1 3 13 15 5 7
10 8 2 0 14 12 6 4 11 9 3 1 15 13 7 5
4 6 12 14 0 2 8 10 5 7 13 15 1 3 9 11
6 4 14 12 2 0 10 8 7 5 15 13 3 1 11 9
12 14 4 6 8 10 0 2 13 15 5 7 9 11 1 3
14 12 6 4 10 8 2 0 15 13 7 5 11 9 3 1
1 3 9 11 5 7 13 15 0 2 8 10 4 6 12 14
3 1 11 9 7 5 15 13 2 0 10 8 6 4 14 12
9 11 1 3 13 15 5 7 8 10 0 2 12 14 4 6
11 9 3 1 15 13 7 5 10 8 2 0 14 12 6 4
5 7 13 15 1 3 9 11 4 6 12 14 0 2 8 10
7 5 15 13 3 1 11 9 6 4 14 12 2 0 10 8
13 15 5 7 9 11 1 3 12 14 4 6 8 10 0 2
15 13 7 5 11 9 3 1 14 12 6 4 10 8 2 0
M16 = 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15
4 0 12 8 5 1 13 9 6 2 14 10 7 3 15 11
8 12 0 4 9 13 1 5 10 14 2 6 11 15 3 7
12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3
1 5 9 13 0 4 8 12 3 7 11 15 2 6 10 14
5 1 13 9 4 0 12 8 7 3 15 11 6 2 14 10
9 13 1 5 8 12 0 4 11 15 3 7 10 14 2 6
13 9 5 1 12 8 4 0 15 11 7 3 14 10 6 2
2 6 10 14 3 7 11 15 0 4 8 12 1 5 9 13
6 2 14 10 7 3 15 11 4 0 12 8 5 1 13 9
10 14 2 6 11 15 3 7 8 12 0 4 9 13 1 5
14 10 6 2 15 11 7 3 12 8 4 0 13 9 5 1
3 7 11 15 2 6 10 14 1 5 9 13 0 4 8 12
7 3 15 11 6 2 14 10 5 1 13 9 4 0 12 8
11 15 3 7 10 14 2 6 9 13 1 5 8 12 0 4
15 11 7 3 14 10 6 2 13 9 5 1 12 8 4 0
M17 = 0 4 8 12 2 6 10 14 1 5 9 13 3 7 11 15
4 0 12 8 6 2 14 10 5 1 13 9 7 3 15 11
8 12 0 4 10 14 2 6 9 13 1 5 11 15 3 7
12 8 4 0 14 10 6 2 13 9 5 1 15 11 7 3
2 6 10 14 0 4 8 12 3 7 11 15 1 5 9 13
6 2 14 10 4 0 12 8 7 3 15 11 5 1 13 9
10 14 2 6 8 12 0 4 11 15 3 7 9 13 1 5
14 10 6 2 12 8 4 0 15 11 7 3 13 9 5 1
1 5 9 13 3 7 11 15 0 4 8 12 2 6 10 14
5 1 13 9 7 3 15 11 4 0 12 8 6 2 14 10
9 13 1 5 11 15 3 7 8 12 0 4 10 14 2 6
13 9 5 1 15 11 7 3 12 8 4 0 14 10 6 2
3 7 11 15 1 5 9 13 2 6 10 14 0 4 8 12
7 3 15 11 5 1 13 9 6 2 14 10 4 0 12 8
11 15 3 7 9 13 1 5 10 14 2 6 8 12 0 4
15 11 7 3 13 9 5 1 14 10 6 2 12 8 4 0
M18 = 0 8 1 9 2 10 3 11 4 12 5 13 6 14 7 15
8 0 9 1 10 2 11 3 12 4 13 5 14 6 15 7
1 9 0 8 3 11 2 10 5 13 4 12 7 15 6 14
9 1 8 0 11 3 10 2 13 5 12 4 15 7 14 6
2 10 3 11 0 8 1 9 6 14 7 15 4 12 5 13
10 2 11 3 8 0 9 1 14 6 15 7 12 4 13 5
3 11 2 10 1 9 0 8 7 15 6 14 5 13 4 12
11 3 10 2 9 1 8 0 15 7 14 6 13 5 12 4
4 12 5 13 6 14 7 15 0 8 1 9 2 10 3 11
12 4 13 5 14 6 15 7 8 0 9 1 10 2 11 3
5 13 4 12 7 15 6 14 1 9 0 8 3 11 2 10
13 5 12 4 15 7 14 6 9 1 8 0 11 3 10 2
6 14 7 15 4 12 5 13 2 10 3 11 0 8 1 9
14 6 15 7 12 4 13 5 10 2 11 3 8 0 9 1
7 15 6 14 5 13 4 12 3 11 2 10 1 9 0 8
15 7 14 6 13 5 12 4 11 3 10 2 9 1 8 0
M19 = 0 8 2 10 1 9 3 11 4 12 6 14 5 13 7 15
8 0 10 2 9 1 11 3 12 4 14 6 13 5 15 7
2 10 0 8 3 11 1 9 6 14 4 12 7 15 5 13
10 2 8 0 11 3 9 1 14 6 12 4 15 7 13 5
1 9 3 11 0 8 2 10 5 13 7 15 4 12 6 14
9 1 11 3 8 0 10 2 13 5 15 7 12 4 14 6
3 11 1 9 2 10 0 8 7 15 5 13 6 14 4 12
11 3 9 1 10 2 8 0 15 7 13 5 14 6 12 4
4 12 6 14 5 13 7 15 0 8 2 10 1 9 3 11
12 4 14 6 13 5 15 7 8 0 10 2 9 1 11 3
6 14 4 12 7 15 5 13 2 10 0 8 3 11 1 9
14 6 12 4 15 7 13 5 10 2 8 0 11 3 9 1
5 13 7 15 4 12 6 14 1 9 3 11 0 8 2 10
13 5 15 7 12 4 14 6 9 1 11 3 8 0 10 2
7 15 5 13 6 14 4 12 3 11 1 9 2 10 0 8
15 7 13 5 14 6 12 4 11 3 9 1 10 2 8 0
M20 = 0 8 1 9 4 12 5 13 2 10 3 11 6 14 7 15
8 0 9 1 12 4 13 5 10 2 11 3 14 6 15 7
1 9 0 8 5 13 4 12 3 11 2 10 7 15 6 14
9 1 8 0 13 5 12 4 11 3 10 2 15 7 14 6
4 12 5 13 0 8 1 9 6 14 7 15 2 10 3 11
12 4 13 5 8 0 9 1 14 6 15 7 10 2 11 3
5 13 4 12 1 9 0 8 7 15 6 14 3 11 2 10
13 5 12 4 9 1 8 0 15 7 14 6 11 3 10 2
2 10 3 11 6 14 7 15 0 8 1 9 4 12 5 13
10 2 11 3 14 6 15 7 8 0 9 1 12 4 13 5
3 11 2 10 7 15 6 14 1 9 0 8 5 13 4 12
11 3 10 2 15 7 14 6 9 1 8 0 13 5 12 4
6 14 7 15 2 10 3 11 4 12 5 13 0 8 1 9
14 6 15 7 10 2 11 3 12 4 13 5 8 0 9 1
7 15 6 14 3 11 2 10 5 13 4 12 1 9 0 8
15 7 14 6 11 3 10 2 13 5 12 4 9 1 8 0
M21 = 0 8 2 10 4 12 6 14 1 9 3 11 5 13 7 15
8 0 10 2 12 4 14 6 9 1 11 3 13 5 15 7
2 10 0 8 6 14 4 12 3 11 1 9 7 15 5 13
10 2 8 0 14 6 12 4 11 3 9 1 15 7 13 5
4 12 6 14 0 8 2 10 5 13 7 15 1 9 3 11
12 4 14 6 8 0 10 2 13 5 15 7 9 1 11 3
6 14 4 12 2 10 0 8 7 15 5 13 3 11 1 9
14 6 12 4 10 2 8 0 15 7 13 5 11 3 9 1
1 9 3 11 5 13 7 15 0 8 2 10 4 12 6 14
9 1 11 3 13 5 15 7 8 0 10 2 12 4 14 6
3 11 1 9 7 15 5 13 2 10 0 8 6 14 4 12
11 3 9 1 15 7 13 5 10 2 8 0 14 6 12 4
5 13 7 15 1 9 3 11 4 12 6 14 0 8 2 10
13 5 15 7 9 1 11 3 12 4 14 6 8 0 10 2
7 15 5 13 3 11 1 9 6 14 4 12 2 10 0 8
15 7 13 5 11 3 9 1 14 6 12 4 10 2 8 0
M22 = 0 8 4 12 1 9 5 13 2 10 6 14 3 11 7 15
8 0 12 4 9 1 13 5 10 2 14 6 11 3 15 7
4 12 0 8 5 13 1 9 6 14 2 10 7 15 3 11
12 4 8 0 13 5 9 1 14 6 10 2 15 7 11 3
1 9 5 13 0 8 4 12 3 11 7 15 2 10 6 14
9 1 13 5 8 0 12 4 11 3 15 7 10 2 14 6
5 13 1 9 4 12 0 8 7 15 3 11 6 14 2 10
13 5 9 1 12 4 8 0 15 7 11 3 14 6 10 2
2 10 6 14 3 11 7 15 0 8 4 12 1 9 5 13
10 2 14 6 11 3 15 7 8 0 12 4 9 1 13 5
6 14 2 10 7 15 3 11 4 12 0 8 5 13 1 9
14 6 10 2 15 7 11 3 12 4 8 0 13 5 9 1
3 11 7 15 2 10 6 14 1 9 5 13 0 8 4 12
11 3 15 7 10 2 14 6 9 1 13 5 8 0 12 4
7 15 3 11 6 14 2 10 5 13 1 9 4 12 0 8
15 7 11 3 14 6 10 2 13 5 9 1 12 4 8 0
M23 = 0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15
8 0 12 4 10 2 14 6 9 1 13 5 11 3 15 7
4 12 0 8 6 14 2 10 5 13 1 9 7 15 3 11
12 4 8 0 14 6 10 2 13 5 9 1 15 7 11 3
2 10 6 14 0 8 4 12 3 11 7 15 1 9 5 13
10 2 14 6 8 0 12 4 11 3 15 7 9 1 13 5
6 14 2 10 4 12 0 8 7 15 3 11 5 13 1 9
14 6 10 2 12 4 8 0 15 7 11 3 13 5 9 1
1 9 5 13 3 11 7 15 0 8 4 12 2 10 6 14
9 1 13 5 11 3 15 7 8 0 12 4 10 2 14 6
5 13 1 9 7 15 3 11 4 12 0 8 6 14 2 10
13 5 9 1 15 7 11 3 12 4 8 0 14 6 10 2
3 11 7 15 1 9 5 13 2 10 6 14 0 8 4 12
11 3 15 7 9 1 13 5 10 2 14 6 8 0 12 4
7 15 3 11 5 13 1 9 6 14 2 10 4 12 0 8
15 7 11 3 13 5 9 1 14 6 10 2 12 4 8 0
|