3-ary Boolean functions

Studies of Boolean functions

There are $2^{2^{3}}$ = 256 3-ary Boolean functions, like set operations or logical connectives.

The 3-ary Boolean function $\scriptstyle (A\land \neg C)\lor (B\land C)$ represented as a Venn diagram

sec 53 containing 8 functions, including the one shown above (shown in the top right position)

bec 27 containing 3 secs, including the one shown above (shown in orange)

The 22 becs ordered by weight, including the one shown above (shown second on the left in box 4)
Compare  A039754

This Venn diagram , representing the intersection of 3 sets, or the conjunction of 3 statements respectively, gives an example of a 3-ary Boolean function.

Equivalence classes

See: Equivalence classes of Boolean functions

The set of 256 functions can be parted into various equivalence classes.
The most basic way to do that are the 46 small equivalence classes (secs). Functions belong to the same sec, when they can be expressed by each other by negating arguments. There are 3 arguments that can be negated, so there can be up to $2^{3}$ = 8 different functions in a sec.

When binarily colored cubes can be transformed into each other by mirroring and rotation, they are essentially the same.
The corresponding Boolean functions are often called equivalent and belong to the same big equivalence class (bec).

Numbers of equivalence classes

wec: 5
sec:  A000231(3) = 46	bec:  A000616(3) = 22
gsec: 30	gbec: 14
ggsec: 18	ggbec: 8

The following sequences show the number of secs and becs by weight:

                weight   =   0   1   2   3   4   5   6   7   8
secs: A054724(3, 0..8)   =   1   1   7   7  14   7   7   1   1
becs: A039754(3, 0..8)   =   1   1   3   3   6   3   3   1   1

The following sequences show the number of secs and becs by number of functions in each sec:

                             1    2    4    8
secs: A227725(3, 0..3)   =   2    7   14   23
becs:                        2    3    6   11

Permutations of functions in a bec

Theoretically a bec could have 3! * 2³ = 6 * 8 = 48 functions, but the largest becs have only 24. (There are some becs of 4-ary functions with the highest possible number of functions, e.g. this one.)

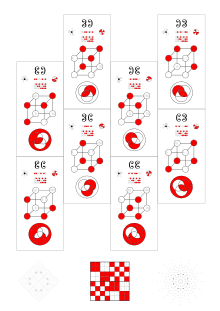
permuting all 3 arguments
3 4

permutations of functions in a sec
Cycle graph of S3 Each of the six files corresponds to a permutation of (A, B, C).	0	All 48 permutations in the cycle graph of the full octahedral group

permuting 2 arguments
1 5 2

Nonlinearity

The nonlinearity of a function is the smallest Hamming distance it has from one of the 16 linear functions, i.e. from a row of the binary Walsh matrix or its complement.
The functions in wec E0 are the linear functions, i.e. those with nonlinearity 0. The functions in wec O have nonlinearity 1, and all others have nonlinearity 2.
There are no 3-ary bent functions.

Nonlinearity
The 8 functions in the Walsh matrix and their complements are linear.	$\scriptstyle (A\lor B)\land \neg C$ in sec 7 has nonlinearity 1.	$\scriptstyle (\neg A\lor \neg C)\land (\neg B\lor C)$ in sec 53 has nonlinearity 2.

Walsh spectrum

The Boolean function $\scriptstyle (1,0,1,0,0,1,1,0)$
has the Walsh spectrum $\scriptstyle (4,2,0,-2,0,2,0,2)$
and the binary Walsh spectrum $\scriptstyle (0,1,0,1,0,1,0,1)$. The latter is row 1 of the Walsh matrix.

The Walsh spectrum of a Boolean function is the product of its binary string (as a row vector) with a Walsh matrix.
The first entry of the Walsh spectrum is the functions digit sum, and all entries have the same parity.

In the following chapter Walsh spectra are shown in the "by ggbec" sections.
Walsh spectra of the same sec (which differ only in the signs of their entries) are always shown in the same file.

The Walsh spectra of complements sum up to $\scriptstyle (8,0,0,0,0,0,0,0,)$.

Walsh matrix with row numbers

Further the binary Walsh spectra are always shown by the red squares in the background. They are always rows of a binary Walsh matrix - or, in other terms, exclusive disjunctions of unnegated arguments.

The functions with odd digit sum, which make up wec O, have each binary Walsh spectrum one time in every sec.

The functions with even digit sum, which make up the other four wecs, have always the same binary Walsh spectrum in the same sec:

$\scriptstyle \oplus ()$

= 0000 0000

in wec E0

$\scriptstyle \oplus (A)$

= 0101 0101

or

$\scriptstyle \oplus (B)$

= 0011 0011

or

$\scriptstyle \oplus (C)$

= 0000 1111

in wec E1

$\scriptstyle \oplus (A,B)$

= 0110 0110

or

$\scriptstyle \oplus (A,C)$

= 0101 1010

or

$\scriptstyle \oplus (B,C)$

= 0011 1100

in wec E2

$\scriptstyle \oplus (A,B,C)$

= 0110 1001

in wec E3

Functions with the same binary Walsh spectrum

In the diagrams in this section the even functions are shown in red, and the odd ones (i.e. those in wec O) in yellow. Each odd function differs in the lowest bit (numerically: by 1) from an even function with the same binary Walsh spectrum. So in the octeract graphs each red vertex is connected to a yellow vertex by an edge of the direction corresponding to the lowest bit (like the edge connecting vertices 0 and 1). The pattern of the red vertices is always symmetrical to the main axes. Surprisingly the yellow vertices are also symmetrical, but to axes tilted to the left or to the right (indicated by \ or / in the table).

3
\ 7

2
\ 3 / 5 \ 6

1
/ 1 \ 2 / 4

0
/ 0

Nested equivalence classes

Overview

The matrix on the right shows the 256 functions arranged in a way similar to the Hasse diagram, which is an octeract graph.
The colors indicate the five wecs, as shown in the table below.

The two following matrices are examples of a gbec and a ggsec. Both contain the sec 26. Files like these are in the collapsible boxes below in boxes labeled Positions.

These matrices are symmetric to the main diagonal, because they contain complete secs. They are also symmetric to the antidiagonal, because they contain all the complements, and complements are symmetric about the center of the matrix. The ggsec matrices are also symmetric about the central axes, because they contain all the half-complements. Left half-complements are vertically, and right ones are horizontally symmetric to each other.

gbec 25 with 6 secs (sec 26 is light green)

ggsec 21 with 4 secs (sec 26 is light red)

Hasse diagram and diamond matrix
The Hasse diagram of the 256 functions ordered by implication is an 8-dimensional cube or octeract, here represented in its Petrie polygon projection.	The same matrix as above in diamond orientation — Instead of decimal numbers it shows the nibble shorthands that are also used in the sec files.
On the bottom of each sec file (e.g. this one) the positions of the functions are shown in the octeract graph and the diamond matrix.

O nonlinearity 1	E0   nonlinearity 0	E1   nonlinearity 2	E2   nonlinearity 2	E3   nonlinearity 2
by ggbec        ggbec 1 with 64 functions        ggbec 22 with 64 functions	by ggbec ggbec 0 with 2 functions ggbec 15 with 6 functions        ggbec 60 with 8 functions	by ggbec        ggbec 3 with 48 functions	by ggbec        ggbec 6 with 48 functions	ggbec 23 with 16 functions
by ggsec	by ggsec	by ggsec	by ggsec
1 22 1 7 22 25 1 127 7 31 22 107 25 61 1 1 1 8 127 8 7 7 8 31 8 19 19 19 8 55 8 28 28 8 61 8 21 21 21 8 87 8 26 26 8 91 8 22 22 22 8 107 8 25 25 8 103 8	0 15 60 0 15 60 105 0 255 15 60 105 0 0 0 1 255 1 15 15 2 51 51 51 2 60 60 2 85 85 85 2 90 90 2 102 102 102 2 105 105 2	3 3 30 3 63 30 3 3 3 4 63 4 5 5 5 4 95 4 17 17 17 4 119 4 30 30 8 54 54 54 8 86 86 86 8	6 6 27 6 111 27 6 6 6 4 111 4 18 18 18 4 123 4 29 29 8 20 20 20 4 125 4 27 27 8 53 53 53 8	23 23 24 23 24 126 23 23 23 8 24 24 4 126 4

The tables above show how the equivalence classes are nested in each other. Each table shows the equivalence classes in a wec.
The vertical axes show ggsecs, gsecs and secs, and the horizontal ones show ggbecs, gbecs and becs.
The entries in the matrices show which secs belong to which becs.
The numbers in these fields show how many functions are in each sec. A dark red background tells that the sec contains a monotonic function.

wec O with 128 functions

wec O ordered by ggbec

wec O ordered by ggbec

ggbec 1 with 64 functions gbec 1 with 16 functions N(0) bec 1 with 8 functions sec 1 with 8 functions $\scriptstyle A\land B\land C$ bec 127 with 8 functions sec 127 with 8 functions $\scriptstyle A\lor B\lor C$ Positions Walsh spectra gbec 7 with 48 functions N(0) bec 7 with 24 functions sec 7 with 8 functions $\scriptstyle (A\lor B)\land C$ sec 19 with 8 functions $\scriptstyle (C\lor A)\land B$ sec 21 with 8 functions $\scriptstyle (B\lor C)\land A$ bec 31 with 24 functions sec 31 with 8 functions $\scriptstyle (A\land B)\lor C$ sec 55 with 8 functions $\scriptstyle (C\land A)\lor B$ sec 87 with 8 functions $\scriptstyle (B\land C)\lor A$ Positions Walsh spectra ggbec 22 with 64 functions gbec 22 with 16 functions N(0) bec 22 with 8 functions sec 22 with 8 functions $\scriptstyle (A\lor B)\land (A\lor C)\land (B\lor C)\land (\neg A\lor \neg B\lor \neg C)$ bec 107 with 8 functions sec 107 with 8 functions $\scriptstyle (A\land B)\lor (A\land C)\lor (B\land C)\lor (\neg A\land \neg B\land \neg C)$ Positions Walsh spectra gbec 25 with 48 functions N(0) bec 25 with 24 functions sec 25 with 8 functions $\scriptstyle (A\land B)\lor (\neg A\land \neg B\land C)$ sec 26 with 8 functions $\scriptstyle (C\land A)\lor (\neg C\land \neg A\land B)$ sec 28 with 8 functions $\scriptstyle (B\land C)\lor (\neg B\land \neg C\land A)$ bec 61 with 24 functions sec 103 with 8 functions $\scriptstyle (A\lor B)\land (\neg A\lor \neg B\lor C)$ sec 91 with 8 functions $\scriptstyle (C\lor A)\land (\neg C\lor \neg A\lor B)$ sec 61 with 8 functions $\scriptstyle (B\lor C)\land (\neg B\lor \neg C\lor A)$ Positions Walsh spectra

wec O ordered by ggsec

wec O ordered by ggsec

ggsec 1 with 32 functions gsec 1 with 16 functions 0 in N(0) sec 1 with 8 functions $\scriptstyle A\land B\land C$ sec 127 with 8 functions $\scriptstyle A\lor B\lor C$ gsec 7 with 16 functions 0 in N(0) sec 7 with 8 functions $\scriptstyle (A\lor B)\land C$ sec 31 with 8 functions $\scriptstyle (A\land B)\lor C$ Positions ggsec 19 with 32 functions gsec 28 with 16 functions 0 in N(0) sec 28 with 8 functions $\scriptstyle (B\land C)\lor (A\land \neg B\land \neg C)$ sec 61 with 8 functions $\scriptstyle (B\lor C)\land (A\land \neg B\lor \neg C)$ gsec 19 with 16 functions 0 in N(0) sec 19 with 8 functions $\scriptstyle (A\lor C)\land B$ sec 55 with 8 functions $\scriptstyle (A\land C)\lor B$ Positions ggsec 21 with 32 functions gsec 26 with 16 functions 0 in N(0) sec 26 with 8 functions $\scriptstyle (A\land C)\lor (\neg A\land B\land \neg C)$ sec 91 with 8 functions $\scriptstyle (A\lor C)\land (\neg A\lor B\lor \neg C)$ gsec 21 with 16 functions 0 in N(0) sec 21 with 8 functions $\scriptstyle (B\lor C)\land A$ sec 87 with 8 functions $\scriptstyle (B\land C)\lor A$ Positions ggsec 22 with 32 functions gsec 25 with 16 functions 0 in N(0) sec 25 with 8 functions $\scriptstyle (A\land B)\lor (\neg A\land \neg B\land C)$ sec 103 with 8 functions $\scriptstyle (A\lor B)\land (\neg A\lor \neg B\lor C)$ gsec 22 with 16 functions 0 in N(0) sec 22 with 8 functions $\scriptstyle (A\lor B)\land (A\lor C)\land (B\lor C)\land (\neg A\lor \neg B\lor \neg C)$ sec 107 with 8 functions $\scriptstyle (A\land B)\lor (A\land C)\lor (B\land C)\lor (\neg A\land \neg B\land \neg C)$ Positions

wec E0 with 16 functions

wec E0 ordered by ggbec

wec E0 ordered by ggbec

ggbec 0 = gbec 0 with 2 functions N(3, 1) bec 0 with 1 function sec 0 with 1 function $\scriptstyle X\land \neg X$ bec 255 with 1 function sec 255 with 1 function $\scriptstyle X\lor \neg X$ Positions Walsh spectra ggbec 15 = gbec 15 = bec 15 with 6 functions N(2, 1) sec 15 with 2 functions $\scriptstyle C$ sec 51 with 2 functions $\scriptstyle B$ sec 85 with 2 functions $\scriptstyle A$ Positions Walsh spectra ggbec 60 with 8 functions gbec 60 = bec 60 with 6 functions N(2, 2) sec 102 with 2 functions $\scriptstyle A\leftrightarrow B$ sec 90 with 2 functions $\scriptstyle A\leftrightarrow C$ sec 60 with 2 functions $\scriptstyle B\leftrightarrow C$ gbec 105 = bec 105 with 2 functions N(2, 3) sec 105 with 2 functions $\scriptstyle A\oplus B\oplus C$ Positions Walsh spectra

wec E0 ordered by ggsec

wec E0 ordered by ggsec

ggsec 0 with 4 functions gsec 0 with 2 functions 15 in N(3, 1) sec 0 with 1 function $\scriptstyle X\land \neg X$ sec 255 with 1 function $\scriptstyle X\lor \neg X$ gsec 15 with 2 functions 4 in N(2, 1) sec 15 with 2 functions $\scriptstyle C$ Positions ggsec 102 with 4 functions gsec 102 with 2 functions 12 in N(2, 2) sec 102 with 2 functions $\scriptstyle A\leftrightarrow B$ gsec 105 with 2 functions 10 in N(2, 3) sec 105 with 2 functions $\scriptstyle A\oplus B\oplus C$ Positions ggsec 51 with 4 functions gsec 60 with 2 functions 14 in N(2, 2) sec 60 with 2 functions $\scriptstyle B\leftrightarrow C$ gsec 51 with 2 functions 7 in N(2, 1) sec 51 with 2 functions $\scriptstyle B$ Positions ggsec 85 with 4 functions gsec 90 with 2 functions 13 in N(2, 2) sec 90 with 2 functions $\scriptstyle A\leftrightarrow C$ gsec 85 with 2 functions 9 in N(2, 1) sec 85 with 2 functions $\scriptstyle A$ Positions

wec E1 with 48 functions

wec E1 ordered by ggbec

wec E1 = ggbec 3 with 48 functions

gbec 3 with 24 functions N(1, 1) bec 3 with 12 functions sec 17 with 4 functions $\scriptstyle A\land B$ sec 5 with 4 functions $\scriptstyle A\land C$ sec 3 with 4 functions $\scriptstyle B\land C$ bec 63 with 12 functions sec 119 with 4 functions $\scriptstyle A\lor B$ sec 95 with 4 functions $\scriptstyle A\lor C$ sec 63 with 4 functions $\scriptstyle B\lor C$ Positions Walsh spectra gbec 30 = bec 30 with 24 functions N(0) sec 30 with 8 functions $\scriptstyle (A\lor B)\leftrightarrow C$ sec 54 with 8 functions $\scriptstyle (A\lor C)\leftrightarrow B$ sec 86 with 8 functions $\scriptstyle (B\lor C)\leftrightarrow A$ Positions Walsh spectra

wec E1 ordered by ggsec

wec E1 ordered by ggsec

ggsec 17 with 16 functions gsec 17 with 8 functions 5 in N(1, 1) sec 17 with 4 functions $\scriptstyle A\land B$ sec 119 with 4 functions $\scriptstyle A\lor B$ gsec 30 with 8 functions 0 in N(0) sec 30 with 8 functions $\scriptstyle (A\lor B)\leftrightarrow C$ Positions ggsec 3 = gsec 3 with 8 functions 1 in N(1, 1) sec 3 with 4 functions $\scriptstyle B\land C$ sec 63 with 4 functions $\scriptstyle B\lor C$ Positions ggsec 5 = gsec 5 with 8 functions 2 in N(1, 1) sec 5 with 4 functions $\scriptstyle A\land C$ sec 95 with 4 functions $\scriptstyle A\lor C$ Positions ggsec 54 = gsec 54 with 8 functions 0 in N(0) sec 54 with 8 functions $\scriptstyle (A\lor C)\leftrightarrow B$ Positions ggsec 86 = gsec 86 with 8 functions 0 in N(0) sec 86 with 8 functions $\scriptstyle (B\lor C)\leftrightarrow A$ Positions

wec E2 with 48 functions

wec E2 ordered by ggbec

wec E2 = ggbec 6 with 48 functions

gbec 6 with 24 functions N(1, 2) bec 6 with 12 functions sec 6 with 4 functions $\scriptstyle (A\leftrightarrow B)\land C$ sec 18 with 4 functions $\scriptstyle (A\leftrightarrow C)\land B$ sec 20 with 4 functions $\scriptstyle (B\leftrightarrow C)\land A$ bec 111 with 12 functions sec 111 with 4 functions $\scriptstyle (A\oplus B)\lor C$ sec 123 with 4 functions $\scriptstyle (A\oplus C)\lor B$ sec 125 with 4 functions $\scriptstyle (B\oplus C)\lor A$ Positions Walsh spectra gbec 27 = bec 27 with 24 functions N(0) sec 53 with 8 functions $\scriptstyle (A\land \neg C)\lor (B\land C)$ sec 29 with 8 functions $\scriptstyle (C\land \neg B)\lor (A\land B)$ sec 27 with 8 functions $\scriptstyle (B\land \neg A)\lor (C\land A)$ Positions Walsh spectra

wec E2 ordered by ggsec

wec E2 ordered by ggsec

ggsec 20 with 16 functions gsec 20 with 8 functions 8 in N(1, 2) sec 20 with 4 functions $\scriptstyle (B\leftrightarrow C)\land A$ sec 125 with 4 functions $\scriptstyle (B\oplus C)\lor A$ gsec 27 with 8 functions 0 in N(0) sec 27 with 8 functions $\scriptstyle (B\land \neg A)\lor (C\land A)$ Positions ggsec 18 with 16 functions gsec 18 with 8 functions 6 in N(1, 2) sec 18 with 4 functions $\scriptstyle (A\leftrightarrow C)\land B$ sec 123 with 4 functions $\scriptstyle (A\oplus C)\lor B$ gsec 29 with 8 functions 0 in N(0) sec 29 with 8 functions $\scriptstyle (C\land \neg B)\lor (A\land B)$ Positions ggsec 6 = gsec 6 with 8 functions 3 in N(1, 2) sec 6 with 4 functions $\scriptstyle (A\leftrightarrow B)\land C$ sec 111 with 4 functions $\scriptstyle (A\oplus B)\lor C$ Positions ggsec 53 = gsec 53 with 8 functions 0 in N(0) sec 53 with 8 functions $\scriptstyle (A\land \neg C)\lor (B\land C)$ Positions

wec E3 with 16 functions

wec E3 = ggbec 23 = ggsec 23 with 16 functions

gbec 24 = gsec 24 with 8 functions 11 in N(1, 3) sec 24 with 4 functions $\scriptstyle (A\land B\land C)\lor (\neg A\land \neg B\land \neg C)$ sec 126 with 4 functions $\scriptstyle (A\lor B\lor C)\land (\neg A\lor \neg B\lor \neg C)$ gbec 23 = gsec 23 with 8 functions 0 in N(0) sec 23 with 8 functions $\scriptstyle (A\land B)\lor (A\land C)\lor (B\land C)$ $\scriptstyle (A\lor B)\land (A\lor C)\land (B\lor C)$ Positions Walsh spectra

Monotonic functions

Formulas appear when the mouse is moved over the diagram, and the sec files are linked from them. In the sec files the monotonic functions are always in the top right position.

The right Hasse diagram in the file on the right shows the 20 monotonic 3-ary Boolean functions.

If a sec has a monotonic function, all the secs in the gbec and gsec it belongs to also have one. So one can call secs, gbecs and gsecs monotonic, when they contain monotonic functions. There are 6 gbecs and 12 gsecs that are monotonic in this sense. Their collapsible boxes are marked with Tudor roses .

In the above tables that show the nesting of the equivalence classes the monotonic secs have a dark red instead of a black background.

gbec	weight	gsec
0	0, 8	0
1	1, 7	1
3	2, 6	3, 5, 17
7	3, 5	7, 19, 21
15, 23	4	15, 23, 51, 85

All wecs except E2 contain monotonic functions.

Subgroups of nimber addition

See: Subgroups of nimber addition#Z₂³

16 secs with in all 8 + 7*4 + 7*2 + 1 = 51 functions are related to subgroups of nimber addition:

These matrices describe equivalence relations.

These cubes correspond to the matrices' top lines. In the linked files they are always in the bottom left position.

In each sec matrix its leading function appears in a sona pattern. This pattern is 0 in N(0) iff the sec contains 8 different functions. All the other different sona patterns appear only in the sec matrices of the actual sonas between 1 and 15 and their Boolean complements. Each gbec is marked in green with its sona-bec, and each gsec is marked with its sona-sec.

Complements in secs

There are two kinds of secs that are their own complements (i.e. complete gsecs): Those with sona rank 2, marked as N(2, ...), and the following seven secs containing 8 functions each:

Complements in 8-element secs in a cube
The position of the complement in the sec cube corresponds to the position of the sec cube in the big cube. sec 53 wec E2 sec 23 wec E3 sec 86 wec E1 sec 29 wec E2 sec 54 wec E1 sec 27 wec E2 sec 30 wec E1

Gbecs by similarity to 4-ary sec matrix

In the octeract matrices of the gbecs it can be seen, that they belong together in a way that is independent of ggbecs and wecs. Their pattern is part of a sec matrix of one of the five 4-ary exact-value functions. On the left the functions in these gbecs are shown in the Hasse diagram.

0

	0	gbec 0 wec E0	gbec 60 wec E0	gbec 24 wec E3

1

	1, 2, 4, 8	gbec 1 wec O	gbec 25 wec O

gbec 1 and gbec 25 in a cube
sec 103 sec 127 sec 28 sec 91 sec 26 sec 61 sec 1 sec 25

smallest 4-ary sec matrices
1 2 4 8

2

	3, 5, 6, 9, 10, 12	gbec 3 wec E1	gbec 30 wec E1	gbec 6 wec E2	gbec 27 wec E2

gsecs separately
3, 12 gsec 3 gsec 86 gsec 20 gsec 27 b.W.s. 1 b.W.s. 6 5, 10 gsec 5 gsec 54 gsec 18 gsec 29 b.W.s. 2 b.W.s. 5 6, 9 gsec 17 gsec 30 gsec 6 gsec 53 b.W.s. 4 b.W.s. 3

smallest 4-ary sec matrices
3 5 6 9 10 12

3

	7, 11, 13, 14	gbec 7 wec O	gbec 22 wec O

gbec 7 and gbec 22 in a cube
sec 31 sec 107 sec 21 sec 55 sec 19 sec 87 sec 22 sec 7

smallest 4-ary sec matrices
7 11 13 14

4

	15	gbec 15 wec E0	gbec 105 wec E0	gbec 23 wec E3