
|
Review of dot product and a reminder that unit vectors are orthogonal and have unit magnitude.
Since we are in cylindrical coordinates, we use  for distance to the axis to avoid the use of for distance to the axis to avoid the use of  in spherical coordinates. in spherical coordinates.
Define the vector area differential element  using the outward unit normal using the outward unit normal  . .
From the top down, we see the top of the cylinder in what looks like polar coordinates. On the top circle have a 
Also shown in is the curved side of the cylinder. Here the dimensions of the small rectangle are such that  . .
|

|
The unit vectors  are replaced by are replaced by  . .
|

|
Evaluate the integral over the top surface.
|

|
On the curved sides,  . Note that the "odd" term vanishes: . Note that the "odd" term vanishes:


|

|
When doing the integral over the entire surface, it is customary to put a little circle at the center of the integral sign.
|
|
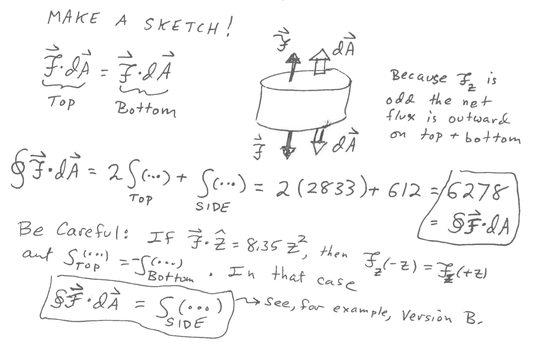
When adding the top and bottom integrals we have to remember that  on the top surface but that on the top surface but that  on the bottom surface. The result depends on whether on the bottom surface. The result depends on whether  is an even or odd function of z. is an even or odd function of z.
|