University of Florida/Eml4500/Lecture Notes
Trusses, Matrix Method
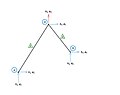
The following image is of a truss with two elastic (deformable) bars.
Note: The displacement at points 1 and 3 is fixed (constrained) to zero, in both the x and the y direction.
Global Free Body Diagram:
The below image illustrates the 4 unknown reactions. This example is statically indeterminate because it has 3 equations and 4 unknown variables. The key to solving this example is to look at the individual bars' deformation.
| Alternate coordinate system |
|---|
|
Instead of choosing the traditional coordinate system, sometimes it is beneficial to choose one at an angle relative to the example that is being solved. If this coordinate system was used, x' would be parallel to one member of the truss, which might prove to be useful. |
2 Free body diagrams of separate bar elements
- Bar Element 1:
| Labeling Explaination |
|---|
|
|
The unknown solutions at the nodes are the nodal degrees of freedom. The choice of nodal degrees depend on the governing differential equation.
- Bar Element 2:
Next step: Force Displacement relationship
The force distance relationship of a 1 dimensional spring element (with one end fixed) is F=KD. (K is the spring constant)
The force displacement relationship of a 1D spring with 2 ends free is as shown above. To solve this more complex problem one needs to use a matrix to relate F=Kd. The matrix for this example is shown below.
Stiffness Matrix:
Case 1: Observer sits on node 1.
- F2=K(d2-d1)
Case 2: Observer sits on node 2, or equilibrium f1+f2=0.
- F1=-F2=-K(d2-d1)=K(d1-d2)
Steps to solve simple truss system.
1.Global Picture (description)
- At structure level:
- Global degrees of freedom (displacement unknowns)
- Global forces
- Actually, the displacement Dofs are partitioned into:
- a known part, e.g., fixed Dof, contraints
- an unknown part: solved by using the finite element method (FEM)
- Similarly, for the forces:
- known part: applied forces
- an unknown part: reactions
2.Element Picture (draw)
- Element Dof (displacements)
- Element forces
- Note: it can be either in global or local coordiante system
3.Global Force-Displacement (FD) relationships
- Element stiffness matrix in global coordinates
- Element force matrices in global coordinates
- Assembley of element stiffness matrices and element force matrices into global FD relation: =
4. Elimination of known Dof to eliminate/reduce the global FD relations (if stiffness matrix is non-singular >> invertable >> det(K) ≠ 0);
Km × m*dm × 1 = F m × 1, where m = n 0 of unknown displacement Dof n = n 0 of known and unknown displacement Dof K is non-singular matix >> K -1 (invertable)>> d m × 1 = K -1 m × m * F m × 1
5.Compute element forces form now known d >> element stresses
6.Compute the reactions (unknown forces)
Example:
-
Excercise
1) Globlal Picture:
-
Global Dof
Numbering of displacement Dof:
- Follow the order of global node numbering. Assume x - axes are horizontal: If horizontal force was considered first in the first global node, then in the consequent nodes the horizontal force should be numbered first as well(vertical force follows the horizontal force in each node force/displacement numbering).