University of Florida/Egm6321/f09.team1.gzc/Mtg10

Mtg 10: Sat, 22 Jan 11

page10-1 HW2.9:Use (1) p.8-1 to generate P5(x), and matlabl command"roots"to comp. the roots of P5(x)to check values in table on  p. 7-5. Plot the roots on [-1,+1] using matlab "plot" command (plot dots "." with coordinator (xi,yi), i = 1,...,5 : use "markersinge" 15) xi: roots of P5(x) yi: Plot  (x, y, '.' , 'markersige' , 15) Repeat the above for P10(x) observe the location of the roots near end points -1 and +1 (prepare for Runge phenomenon) NOTE: Lagrange interp. cont'd p.9-4   page10-2 Simpson's rule (simple) $[a,b]\ x_{0}=a,\ x_{1}={\frac {a+b}{2}},\ x_{2}=b\ \color {red}(1)$ ${\color {blue}{\underline {Method1:}}}\ f_{2}(x)=P_{2}(x){\overset {\color {red}(2)}{=}}c_{2}x^{2}+c_{1}x+c_{0}$ c0,  c1,  c2   unknowns p2=(xi) = f(xi)    i= 0, 1, 2               (3) 3 equations for 3 unknowns {ci} Method 2:Use lagrangeinterp.(2) p.8-3   (1) p.9-2   ${\color {red}{(4)}}=\sum _{i=0}^{\color {blue}{n=2}}{\color {blue}{\underset {l_{i}(x)}{\underbrace {\color {black}l_{i,2}(x)} }}}f(x_{i})$ Equiv. 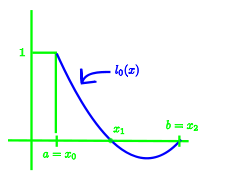of meth1 and meth 2:            (3)   $p_{2}(x_{j})=\sum _{i=0}^{2}\color {blue}{\underset {\delta _{ij}}{\underbrace {\color {black}l_{i}(x_{j})} }}f(x_{i})=f{x_{j}}\ \color {red}(5)$ page10-3 $l_{0{\color {blue},2}}=l_{0{\color {blue},2}}=\prod _{j=0{\color {red}j\neq i}}^{n=2}{\frac {x-x_{j}}{x_{0}-x_{j}}}={\frac {(x-x_{1})(x-x_{2})}{(x_{0}-x_{1})(x_{0}-x_{2})}}\ {\color {blue}\in P_{2}}$ It can be verified that l0(x0)=1 , l0(x1) = l0(x2) = 0 li(xj) = δij                  i,j = 0. 1. 2 ${\color {blue}{\underset {\color {blue}l_{1}(x)}{\underbrace {\color {black}l_{1{\color {blue}(i=1),2(n=2)}}(x)} }}}=\prod _{j=0,{\color {red}{j\neq 1}}}^{2{\color {blue}(n=2)}}{\frac {x-x_{j}}{x_{i{\color {blue}(i=1)}}-x_{j}}}={\frac {(x-x_{0})(x-x_{2})}{{\color {blue}{\underset {>0}{\underbrace {\color {black}(x_{1}-x_{0})} }}}{\color {blue}{\underset {<0}{\underbrace {\color {black}(x_{1}-x_{2})} }}}}}\ {\color {blue}\in P_{2}}$ $l_{1}(x_{1})=1\ ,\ l_{1}(x_{0})=l_{1}(x_{2})=0$ page10-4 ${l}_{1}^{''}(x_{1})<0$ HW*2.10: Use(2) & (3)p.10-2 to find expression for {ci} in terms (xi, f(xi)) i=0,1,2. HW*2.11: Use (4) p.10-2 to derive simple Simpson's rule HW*2.11:f(x)-ex1/x on [o,1] S10and on [-1,1]S11 Consider n=1(Trap), 2(Simp), 4, 8, 16   page10-5 Constrast fn(x) as in (2) p.8-3. Plot f , fn , n= 1, 2, 4, 8, 16 Compare ${I}_{n}=\int _{a}^{b}f_{n}(x)dx$ n=1, 2, 4, 8 and compare to I (use WA with more digits) For n=5 plot l0, l1, l2 How would l3, l4, l5  look like? HW*2.13:show ${\underset {Simple\ Trap.}{\underbrace {{\color {red}(1)}{\color {blue}p.7-3}} }}\Rightarrow {\underset {Compare\ Trap.}{\underbrace {{\color {red}(1)}{\color {blue}p.7-4}} }}$ ${\underset {Simple\ Trap.}{\underbrace {{\color {red}(2)}{\color {blue}p.7-4}} }}\Rightarrow {\underset {Compare\ Trap.}{\underbrace {{\color {red}(4)}{\color {blue}p.7-4}} }}$