Template:Tesseract family
In geometry, this family of uniform 4-polytopes has diploid hexadecachoric symmetry,[1] [4,3,3], of order 24*16=384: 4!=24 permutations of the four axes, 24=16 for reflection in each axis. There are 3 small index subgroups, with the first two generate uniform 4-polytopes which are also repeated in other families, [1+,4,3,3], [4,(3,3)+], and [4,3,3]+, all order 192.
| B4 symmetry polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | tesseract | rectified tesseract |
truncated tesseract |
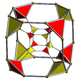
cantellated tesseract |
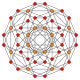
runcinated tesseract |
bitruncated tesseract |
cantitruncated tesseract |
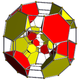
runcitruncated tesseract |
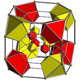
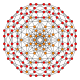
omnitruncated tesseract | ||
| Coxeter diagram |
= |
= |
|||||||||
| Schläfli symbol |
{4,3,3} | t1{4,3,3} r{4,3,3} |
t0,1{4,3,3} t{4,3,3} |
t0,2{4,3,3} rr{4,3,3} |
t0,3{4,3,3} | t1,2{4,3,3} 2t{4,3,3} |
t0,1,2{4,3,3} tr{4,3,3} |
t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegel diagram |

|

|
|

|

|

|
|
|

| ||
| B4 | 
|

|

|

|
|

|

|
|

| ||
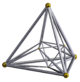
| Name | 16-cell | rectified 16-cell |
truncated 16-cell |
cantellated 16-cell |
runcinated 16-cell |
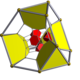
bitruncated 16-cell |
cantitruncated 16-cell |
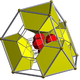
runcitruncated 16-cell |
omnitruncated 16-cell | ||
| Coxeter diagram |
= |
= |
= |
= |
= |
= |
|||||
| Schläfli symbol |
{3,3,4} | t1{3,3,4} r{3,3,4} |
t0,1{3,3,4} t{3,3,4} |
t0,2{3,3,4} rr{3,3,4} |
t0,3{3,3,4} | t1,2{3,3,4} 2t{3,3,4} |
t0,1,2{3,3,4} tr{3,3,4} |
t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegel diagram |
|

|

|

|

|
|

|
|

| ||
| B4 | 
|

|

|

|

|

|

|

|

| ||
References
edit- ↑ Johnson (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups