Quantum mechanics/Photoelectric effect

Instructions on Lab

This essay serves as an introduction to the PhET simulation of the photoelectric effect at PhET (associated with the University of Coloradoa at Boulder). The simulation can by found at

http://phet.colorado.edu/en/simulation/photoelectric

History

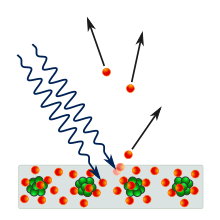
In the photoelectric effect, electrons are emitted from solids, liquids or gases when they absorb energy from light. Electrons emitted in this manner may be called photoelectrons.

In 1887, Heinrich Hertz discovered that electrodes illuminated with ultraviolet light create electric sparks more easily. In 1905 Albert Einstein published a paper that explained experimental data from the photoelectric effect as being the result of light energy being carried in discrete quantized packets. This discovery led to the quantum revolution (and a Nobel Prize for Einstein in 1921). The photoelectric effect depends on the "particle picture" of light in that it seems to confirm Max Planck's previous discovery of the Planck relation linking energy (E) and frequency and Planck constant. These quanta, or discrete values of energy associated with light waves have energy equal to

E=hf

where $f$ is the frequency (cycles per second) of the light striking the metal plate, and $h$ is Planck’s constant.

Experimental observations of photoelectric emission

For a given metal, there exists a certain minimum frequency of incident radiation below which no photoelectrons are emitted. This frequency is called the threshold frequency. Increasing the frequency of the incident beam, keeping the number of incident photons fixed (this would result in a proportionate increase in energy) increases the maximum kinetic energy of the photoelectrons emitted. Thus the stopping voltage increases. If the intensity of the incident radiation is increased, there is no effect on the kinetic energies of the photoelectrons. The kinetic energy depends only on the frequency on the light, and hence the energy provided by each photon. This suggests that the photoelectric effect involves one electron and only one photon.

Above the threshold frequency, the maximum kinetic energy energy of the emitted photoelectron depends on the frequency of the incident light, but is independent of the intensity of the incident light so long as the latter is not too high. On the other hand, the stopping voltage does not depend on the intensity of the light (provided the light's frequency is kept fixed.)

Mathematical description

Here we show how the work function of the metal, as well as the numerical value of Plank's constant can be experimentally deduced from a plot of stopping voltage versus photon frequency. The maximum kinetic energy $K_{\mathrm {max} }$ equals the energy that the electron received from the photon minus the energy required to remove the electron from the metal.

K_{\mathrm {max} }=h\,f-\varphi ,

where $h$ is the Planck constant and $f$ is the frequency of the incident photon. The term $\varphi$ is the work function, which gives the minimum energy required to remove a delocalised electron from the surface of the metal.

The important feature of this equation is that it resembles the formula for a straight line ( $y=mx+b$ ). The maximum kinetic energy can be calculated using the voltage required to prevent the electrons from passing between the two electrodes. This minimum voltage to stop all electrons is called the stopping voltage. Plank's constant can be calculated as the slope when stopping voltage is plotted as a function of frequency.

It is interesting how a straight line of a graph of stopping voltage versus frequency is used to measure one of the most mysterious fundamental constants in nature.

Contrasting the Quantum and Classical Models

A classical wave delivering energy to a classical particle. Here, the energy delivered to an electron depends on wave amplitude, which is in contrast to experimental evidence

Ultimately, the quantum theory has to be accepted not because it is logical, but because it describes reality. And, there is one more reason to accept quantum theory: Classical physics fails! If classical physics could explain the photoelectric effect there would be no need for a new theory. How would light interact with the electrons in a metal if the classical theory were valid?

What light would do under a classical model

The equations would be complicated, but this is what a simple application of classical physics to the photoelectric effect would predict:

The light intensity would play a role

Maxwell's equations inform us that electromagnetic waves (i.e., "light") interacts with the electron by exerting a force on the electron. This force is due to the oscillating electric field. But if Newton's law of motion (F=ma) held, electrons would gain enough energy to leave the metal only if the intensity of the light reaches a certain threshold. Instead the experimental evidence suggests a threshold frequency is required.

An adult pushes the girl at every swing by matching the "pushing" frequency to the "natural" frequency of the swing. Significant energy can be delivered, even by a frail old grandparent.

Resonance might play a role

The classical theory does provide for electrons to receive more energy from the light if a resonance occurs. To imagine such a resonance, suppose the electron behaved as if attached to some sort of spring (in reality the spring would be due to interactions between electrons and the atoms in the metal). When a mass is attached to a spring it naturally oscillates at a frequency known as the natural frequency. But if a resonance is responsible for delivering energy to the electrons, light would be more apt to excite photoelectrons at a certain specific frequency, namely at a frequency that matches the natural frequency of the electrons in the metal. But this is also not what is seen experimentally. Instead all light at any frequency above the threshold frequency excites photoelectrons.

An adult pushes the girl at every swing by matching the "pushing" frequency to the "natural" frequency of the swing. Significant energy can be delivered, even by a frail old grandparent.

The property of Resonance is that at a particular frequency energy is optimally stored in a system in that each cycle of the forcing function is properly phased with that which has been stored and a buildup of energy occurs. The level of buildup is limited by the dissipation of energy : Damping

Quiz

See the subpage for a quiz on this topic.

Lab

An in-progress lab is underway. Please contribute!

References

Some of this material was lifted out of wikipedia https://en.wikipedia.org/wiki/Photoelectric_effect
See also Quantum mechanics/Timeline