Physics equations/Rewrite
00-Mathematics for this course
editMeasured in radians, defines angle (in radians), where s is arclength and r is radius. The circumference of a circle is and the circle's area is is its area. The surface area of a sphere is and sphere's volume is

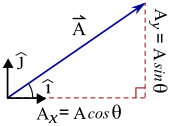
A vector can be expressed as, , where , and are the x and y components. Alternative notation for the unit vectors include and . An important vector is the displacement from the origin, with components are typically written without subscripts: . The magnitude (or absolute value or norm) of a vector is is , where the angle (or phase), , obeys , or (almost) equivalently, . As with any function/inverse function pair, the tangent and arctangent are related by where . The arctangent is not a true function because it is multivalued, with .

The geometric interpretations of and are shown in the figure. Vector addition and subtraction can also be defined through the components: AND
01-Introduction
edit
|
- 1 kilometer = .621 miles and 1 MPH = 1 mi/hr ≈ .447 m/s
- Typically air density is 1.2kg/m3, with pressure 105Pa. The density of water is 1000kg/m3.
- Earth's mean radius ≈ 6371km, mass ≈ 6×1024
kg, and gravitational acceleration = g ≈ 9.8m/s2 - Universal gravitational constant = G ≈ 6.67×10−11
m3·kg−1·s−2 - Speed of sound ≈ 340m/s and the speed of light = c ≈ 3×108m/s
- One light-year ≈ 9.5×1015m ≈ 63240AU (Astronomical unit)
- The electron has charge, e ≈ 1.6 × 10−19C and mass ≈ 9.11 × 10-31kg. 1eV = 1.602 × 10-19J is a unit of energy, defined as the work associated with moving one electron through a potential difference of one volt.
- 1 amu = 1 u ≈ 1.66 × 10-27 kg is the approximate mass of a proton or neutron.
- Boltzmann's constant = kB≈ 1.38 × 10-23 J K−1 , and the gas constant is R = NAkB≈8.314 J K−1 mol−1, where NA≈ 6.02 × 1023 is the Avogadro number.
- ≈ 8.987× 109 N·m²·C−2 is a fundamental constant of electricity; also ≈ 8.854 × 10−12 F·m−1 is the vacuum permittivity or the electric constant.
- = 4π × 10−7 NA ≈ 1.257 × 10−6 N A (magnetic permeability) is the fundamental constant of magnetism: .
- = h/(2π) ≈ 1.054×10−34 J·s the reduced Planck constant, and ≈ .526 × 10−10 m is the Bohr radius.
03-Two-Dimensional Kinematics
edit...in advanced notation this becomes .
In free fall we often set, ax=0 and ay= -g. If angle is measured with respect to the x axis:
not needed 2nd semester
|
|---|
|
The figure shows a Man moving relative to Train with velocity, , where the velocity of the train relative to Earth is, is the velocity of the Train relative to Earth. The velocity of the Man relative to Earth is,
04-Dynamics: Force and Newton's LawseditNewton's laws of motion, can be expressed with two equations, and . The second represents the fact that the force that the i-th object exerts one object exerts on the j-th object is equal and opposite the force that the j-th exerts on the i-th object. 05-Friction, Drag, and Elasticityedit
Also, air drag often depends on speed, an effect this model fails to capture. |
06-Uniform Circular Motion and Gravitation
edit- relates the radian, degree, and revolution.
- is the number of revolutions per second, called frequency.
- is the number of seconds per revolution, called period. Obviously .
- is called angular frequency (ω is called omega, and θ is measured in radians). Obviously
- is the acceleration of uniform circular motion, where v is speed, and r is radius.
- is the force of gravity between two objects, where G ≈ 6.674 × 10-11 m3·kg−1·s−2.
07-Work and Energy
edit- is kinetic energy, where m is mass and v is speed..
- is gravitational potential energy,where y is height, and is the gravitational acceleration at Earth's surface.
- is the potential energy stored in a spring with spring constant .
- relates the final energy to the initial energy. If energy is lost to heat or other nonconservative force, then Q>0.
- (measured in Joules) is the work done by a force as it moves an object a distance . The angle between the force and the displacement is θ.
- describes the work if the force is not uniform. The steps, , taken by the particle are assumed small enough that the force is approximately uniform over the small step. If force and displacement are parallel, then the work becomes the area under a curve of F(x) versus x.
- is the power (measured in Watts) is the rate at which work is done. (v is velocity.)
not needed second semester
| ||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
08-Linear Momentum and Collisionsedit
09-Statics and Torqueedit
10-Rotational Motion and Angular Momentumedit
11-Fluid staticsedit
12-Fluid dynamicsedit
13-Temperature, Kinetic Theory, and Gas Lawsedit
14-Heat and Heat Transferedit
15-Thermodynamicsedit
A point on a PV diagram define's the system's pressure (P) and volume (V). Energy (E) and pressure (P) can be deduced from equations of state: E=E(V,P) and T=T(V,P). If the piston moves, or if heat is added or taken from the substance, energy (in the form of work and/or heat) is added or subtracted. If the path returns to its original point on the PV-diagram (e.g., 12341 along the rectantular path shown), and if the process is quasistatic, all state variables (P, V, E, T) return to their original values, and the final system is indistinguishable from its original state. The net work done per cycle is area enclosed by the loop. This work equals the net heat flow into the system, (valid only for closed loops). Remember: Area "under" is the work associated with a path; Area "inside" is the total work per cycle.
CALCULUS: .
16-Oscillatory Motion and Wavesedit
Let describe position:
17-Physics of Hearingedit
|
18-Electric charge and field
edit- is Coulomb's law for the force between two charged particles separated by a distance r: ke≈8.987×109N·m²·C−2, and ε0≈8.854×10−12 F·m−1.
- is the electric force on a "test charge", q, where is the magnitude of the electric field situated a distance r from a charge, Q.
Consider a collection of particles of charge , located at points (called source points), the electric field at (called the field point) is:
- is the electric field at the field point, , due to point charges at the source points, , and points from source points to the field point.
CALCULUS supplement:
is the electric field due to distributed charge, where , and denote linear, surface, and volume density (or charge density), respectively.
Cartesian coordinates (x, y, z). Volume element: . Line element: . Three basic area elements: , or, , or, .
Cylindrical coordinates (ρ, φ, z): Volume element: . Line element: . Basic area elements: (side), and, (top end).
Spherical coordinates (r, θ, φ): Volume element: (if symmetry holds). Line element: . Basic area element of a sphere: , where dΩ is a solid angle.
19-Electric Potential and Electric Field
edit- is the potential energy of a particle of charge, q, in the presence of an electric potential V.
- (measured in Volts) is the variation in electric potential as one moves through an electric field . The angle between the field and the displacement is θ. The electric potential, V, decreases as one moves parallel to the electric field.
- describes the electric potential if the field is not uniform.
- due to a set of charges at where .
- is the (equal and opposite) charge on the two terminals of a capacitor of capicitance, C, that has a voltage drop, V, across the two terminals.
- is the capacitance of a parallel plate capacitor with surface area, A, and plate separation, d. This formula is valid only in the limit that d2/A vanishes. If a dielectric is between the plates, then ε>ε0≈ 8.85 × 10−12 due to shielding of the applied electric field by dielectric polarization effects.
- is the energy stored in a capacitor.
- is the energy density (energy per unit volume, or Joules per cubic meter) of an electric field.
calculus supplement not needed for exams
|
|---|
|
CALCULUS supplement To the left are closed surfaces. To the right are open surfaces, Ω, that possess closed boundaries, ∂Ω.
Here, Ω is a (3-dimensional) volume and ∂Ω is the boundary of the volume, which is a (two-dimensional) surface. Also a surface is Σ, which, if open, has the boundary ∂Σ, which is a (one-dimensional) curve. |
- in the limit that the Riemann sum becomes an integral.
- where is the del operator.
- is Gauss's law for the surface integral of the electric field over any closed surface, and is the total charge inside that surface.
- is a useful variant if the medium is dielectric. D=εE is the electric displacement field. The permittivity, ε = (1+χ)ε0, where ε0≈ 8.85 × 10−12, and the electric susceptibility, χ, represents the degree to which the medium can be polarized by an electric field. The free charge, Qfree, represents all charges except those represented by the susceptibility, χ.
Help with Gauss' Laws
editSupplied for you in Test 3
|
|---|
|
Wright State University Lake Campus/2017-9/Phy2410/Help with Gauss' law |
20-Electric Current, Resistance, and Ohm's Law
edit- defines the electric current as the rate at which charge flows past a given point on a wire. The direction of the current matches the flow of positive charge (which is opposite the flow of electrons if electrons are the carriers.)
- is Ohm's Law relating current, I, and resistance, R, to the difference in voltage, V, between the terminals. The resistance, R, is positive in virtually all cases, and if R > 0, the current flows from larger to smaller voltage. Any device or substance that obeys this linear relation between I and V is called ohmic.
- relates the density (n), the charge(q), and the average drift velocity (vdrift) of the carriers. The area (A) is measured by imagining a cut across the wire oriented such that the drift velocity is perpendicular to the surface of the (imaginary) cut.
- expresses the resistance of a sample of ohmic material with a length (L) and area (A). The 'resistivity', ρ ("row"), is an intensive property of matter.
- Power is energy/time, measured in joules/second or J/s. Often called P (never p). It is measured in watts (W)
- Current is charge/time, measured in coulombs/second or C/s. Often called I or i. It is measured in amps or ampheres (A)
- Electric potential (or voltage) is energy/charge, measured in joules/coulomb or J/C. Often called V (sometimes E, emf, ). It is measured in volts (V)
- Resistance is voltage/current , measured in volts/amp or V/A. Often called R (sometimes r, Z) It is measured in Ohms (Ω).
- is the power dissipated as current flows through a resistor
21-Circuits, Bioelectricity, and DC Instruments
edit- and are Kirchoff's Laws[3]
- for the voltage divider shown.
- Simple RC circuit[4] The figure to the right depicts a capacitor being charged by an ideal voltage source. If, at t=0, the switch is thrown to the other side, the capacitor will discharge, with the voltage, V , undergoing exponential decay:
where V0 is the capacitor voltage at time t = 0 (when the switch was closed). The time required for the voltage to fall to is called the RC time constant and is given by
22-Magnetism
edit- is the force on a particle with charge q moving at velocity v with in the presence of a magnetic field B. The angle between velocity and magnetic field is θ and the force is perpeduclar to both velocity and magnetic field by the right hand rule.
- expresses this result as a cross product.
- is the force a straight wire segment of length carrying a current, I.
- expresses thus sum over many segments to model a wire.
- CALCULUS: In the limit that we have the integral, .
- is the magnetic field at a distance r from an infinitely long wire carrying a current, where μ0 = 4π × 10−7 N A. This field points azimuthally around the wire in a direction defined by the right hand rule. Application of the force law on a current element, we have
- is the force between two long wires of length separated by a short distance . The currents are I1 and I2, with the force being attractive if the currents are flowing in the same direction.
Cyclotron motion: For a particle moving perpendicular to B, we have cyclotron motion. Recall that for uniform circular motion, the acceleration is a=v2/r, where r is the radius. Since sin θ =1, Newton's second law of motion (F=ma) yields,
Since, sin θ =0, for motion parallel to a magnetic field, particles in a uniform magnetic field move in spirals at a radius which is determined by the perpendicular component of the velocity:
Hall effect: The Hall effect occurs when the magnetic field, velocity, and electric field are mutually perpendicular. In this case, the electric and magnetic forces are aligned, and can cancel if qE=qvB (since sinθ = 1). Since both terms are porportional to charge, q, the appropriate ratio of electric to magnetic field for null net force depends only on velocity:
- ,
where we have used the fact that voltage (i.e. emf or potential) is related to the electric field and a displacement parallel to that field: ΔV = -E Δs cosθ
CALCULUS supplement:
- and the volume integral , where is current density.
- is Ampere's law relating a closed integral involving magnetic field to the total current enclosed by that path. It is often more convenient to define the magnetic field using (typically called "H") and defined by so that H is measured in Amps/meter:
23-Electromagnetic Induction, AC Circuits, and Electrical Technologies
edit- is a consequence of the magnetic force law as seen in the reference frame of a moving charged object, where E is the electric field perceived by an observer moving at velocity v in the presence of a magnetic vield, B. Also written as, E = vBsinθ, this can be used to derive Faraday's law of induction. (Here, θ is the angle between the velocity and the magnetic field.)
- is the magnetic flux, where θ is the angle between the magnetic field and the normal to a surface of area, A.
- is Faraday's law where t is time and N is the number of turns. The minus sign reminds us that the emf, or electromotive force, acts as a "voltage" that opposes the change in the magnetic field or flux.
24-Electromagnetic Waves
edit- is called the displacement current because it replaces the current density when using Ampère's circuital law to calculate the line integral of the magnetic field around a closed loop.
Maxwell's equations hold for all volumes and closed surfaces. In vacuum, electromagnetic waves travel at the speed, .
The last row relates the volume integral of the charge density to the enclosed charge, and also the surface integral of the current density to the current that pierces the surface (or is enclosed by the closed loop that defines the surface).
25-Geometric Optics
editrelates the focal length f of the lens, the image distance S1, and the object distance S2. The figure depicts the situation for which (S1, S2, f) are all positive: (1)The lens is converging (convex); (2) The real image is to the right of the lens; and (3) the object is to the left of the lens. If the lens is diverging (concave), then f < 0. If the image is to the left of the lens (virtual image), then S2 < 0 .
not this semester
|
|---|
27-Wave Opticsedit
|
Test 4 Condensed Summary
edit- (to find the electric field of a capacitor.) Also,
- (is used to relate electric field to voltage (or emf).)
- (is Amphere's Law with Maxwell's extra term. Note that . Also, if Maxwell's term is absent, it is more convenient to define H as B=μ0 so that
- Basic Capacitor rules: where for a parallal plate capacitor, . A capacitor discharging through a resistor obeys (RC is the "RC decay time").
- To find the electric field sum over the point sources:
where points from source points to the field point .
- ↑ https://en.wikipedia.org/w/index.php?title=Torque&oldid=582917749
- ↑ "Linear Motion vs Rotational motion" (PDF).
- ↑ https //en.wikipedia.org/w/index.php?title=Kirchhoff%27s_circuit_laws&oldid=579357795
- ↑ From https://en.wikipedia.org/w/index.php?title=RC_circuit&oldid=598786790























