| Description[1]
|
Figure |
Moment(s) of inertia
|
| Point mass m at a distance r from the axis of rotation.
|
|

|
Two point masses, M and m, with reduced mass  and separated by a distance, x. and separated by a distance, x.
|
|

|
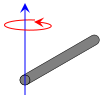
Rod of length L and mass m
(Axis of rotation at the end of the rod)
|
|

|
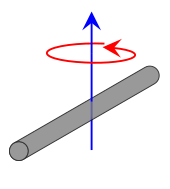
| Rod of length L and mass m
|
|

|
| Thin circular hoop of radius r and mass m
|

|


|
| Thin cylindrical shell with open ends, of radius r and mass m
|

|

|
| Solid cylinder of radius r, height h and mass m
|

|


|
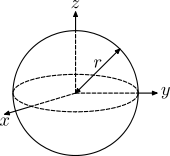
| Sphere (hollow) of radius r and mass m
|
|

|
| Ball (solid) of radius r and mass m
|

|

|
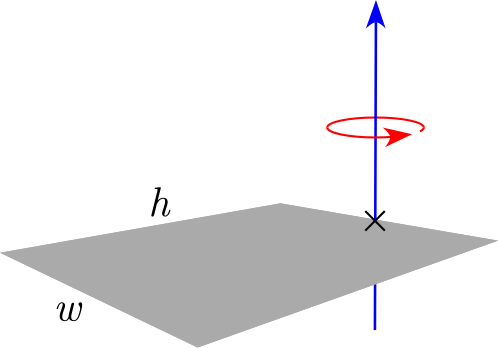
Thin rectangular plate of height h and of width w and mass m
(Axis of rotation at the end of the plate)
|
|

|
| Solid cuboid of height h, width w, and depth d, and mass m
|

|



|
























