Physics equations/06-Uniform Circular Motion and Gravitation/A:proofs

Three proofs are offered for the acceleration of uniform circular motion. A fourth proof involves Kepler's third law, which was used by Newton to conclude that the force law was an inverse-square law.

1. The first uses geometry and for that reason represents a simplified version of how Newton presented the concept to the world.
2. The second uses calculus; this proof is actually easier to learn than the geometrical proof.
3. The inverse square law can be deduced from Kepler's third law. But the inverse square law has deep consequences that allow for Maxwell's equations to exist. This latter statement is not easy to establish, so for now we simply point out the geometric relationship between gravity and butterguns.
4. An advanced discussion allows for curvilinear motion that is neither circular nor uniform; this proof uses methods associated with general relativity.

The amount of butter received by a piece of toast is inversely proportional to the distance from the buttergun used to apply butter to the toast

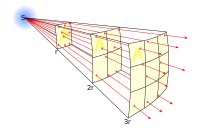
Geometrical proof of equation for uniform circular motion

uniform circular motion (here the Latin d was used instead of the Greek Δ

Using the figure we define the distance traveled by a particle during a brief time interval, $\Delta t$, and the (vector) change in velocity:

1     $\Delta \ell =|{\vec {r}}_{2}-{\vec {r}}_{1}|$, and $\Delta v=|{\vec {v}}_{2}-{\vec {v}}_{1}|$

2     $\Delta \ell =v\Delta t$ (rate times time equals distance).

3     $\Delta {\vec {v}}={\vec {a}}\Delta t$ (definition of acceleration).

4     $\Delta v=a\Delta t$ (taking the absolute value of both sides).

5     ${\frac {\Delta v}{v}}={\frac {\Delta \ell }{r}}$ (by similar triangles). Substituting (2) and (4) yields:

6     ${\frac {a\Delta t}{v}}={\frac {v\Delta t}{r}}$, which leads to ${\frac {a}{v}}={\frac {v}{r}}$, and therefore:

7     $a={\frac {v^{2}}{r}}$

See this quiz based on this proof.

CALCULUS-based proof of formula for uniform circular motion

Let ${\vec {r}}=x{\hat {i}}+y{\hat {j}}=R\cos \omega t{\hat {i}}+R\sin \omega t{\hat {j}}$

Take the derivative twice to get first ${\vec {v}}$ then ${\vec {a}}$:

${\vec {v}}=-\omega R\sin \omega t{\hat {i}}+\omega R\cos \omega t{\hat {j}}$

${\vec {a}}=-\omega ^{2}R\cos \omega t{\hat {i}}-\omega ^{2}R\sin \omega t{\hat {j}}$

Obtain the desired result by taking the magnitude of each vector (i.e. a = (a_x²+a_y²)^1/2).

Derivation of Kepler's third law from the inverse square law

Kepler's third law for circular orbits states that when an object orbits a massive central body, the cube of the distance is proportional to the square of the period. Newton showed that the proportionality constant is proportional to M, the mass of the central body. This allows one to deduce the mass of a planet from the motion of its moons. A generalization to the case where the mass ratio is not large (or small) allows us to deduce the mass of both stars in a binary star system.

1.     $ma=m{\frac {v^{2}}{r}}={\frac {mMG}{r^{2}}}$, where m is the mass of the orbiting object, and M>>m is the mass of the central body, and r is the radius (assuming a circular orbit).
2.     $vT=2\pi r$, where m is the mass of the orbiting object, and M>>m is the mass of the central body, and r is the radius (assuming a circular orbit). After some algebra:
3.     $r^{3}={\frac {MG}{4\pi ^{2}}}T^{2}$

A reveral of these steps allows one to derive the inverse square law from Kepler's third law.

CALCULUS-based (and very advanced) proof of formula for general case (curvilinear motion)

This section is hidden because it is unlikely to appear in an undergraduate physics course

Notational issues with the displacement (r) vector

1. It is often convenient to write vectors in component form, without unit vectors, for example: ${\vec {r}}(t)=\left[\,(x(t),y(t),z(t)\,\right]$
2. The ${\vec {r}}$ is unique in that it's components are not $[r_{x},r_{y},r_{z}]$
3. There exists an irreparable ambiguity regarding differential's of vectors. It is universally recognized that $\Delta r$ represents the differential of the magnitude, $\Delta r\equiv \Delta \left|{\vec {r}}\,\right|$. On the other hand, in uniform circular motion, $|\,v\,|$ is a constant, so it might be more convenient (on board or paper) to write $\Delta v$ as $\left|\Delta {\vec {v}}\,\right|$. So, should we write such non-standard notation into text?

Rigorous discussion of acceleration along a curved path

Here we prove that the acceleration of a particle consists of two parts:

${\vec {a}}={\frac {\rm {dv}}{\rm {dt}}}{\hat {\tau }}+{\frac {v^{2}}{R}}{\hat {\eta }}$

where ${\hat {\eta }}$ and ${\hat {\tau }}$ are unit vectors (called eta-hat and tau-hat); ${\hat {\tau }}$ points tangential to the path, and ${\hat {\eta }}$ points to the center of curvature (perpendicular to ${\hat {\tau }}$). The distance to the center of curvature is R. It is common to use the symbol ${\rm {d\ell }}$ to denote a small change in position. Using component notation for vectors:

${\rm {d{\vec {\ell }}\equiv {\rm {d{\vec {r}}=\left[\,{\rm {dx,{\rm {dy,{\rm {dz\,}}}}}}\right]}}}}$.

Some authorsrefer to this as ${\rm {ds}}$. The scalar magnitude is:

${\rm {d\ell ={\sqrt {dx^{2}+dy^{2}+dz^{2}}}}}$

It is convenient to use dots to denote differential with respect to time:

${\vec {v}}={\frac {d{\vec {x}}}{dt}}\equiv {\dot {\vec {x}}}$

${\vec {a}}={\frac {d{\vec {v}}}{dt}}\equiv {\dot {\vec {v}}}$

Note that $v\equiv |{\vec {v}}|={\frac {d\ell }{dt}}$. Next we define the tangent unit vector ${\hat {\tau }}$, as a unit vector parallel to the velocity:

${\hat {\tau }}={\vec {v}}/v$

We now show that the differential of ${\hat {\tau }}$ is normal (perpendicular) to ${\hat {\tau }}$. We begin by defining the ${\vec {\eta }}$ vector as follows:

${\vec {\eta }}\equiv {\frac {d{\hat {\tau }}}{d\ell }}$

Since (by definition of unit vector) the derivative of ${\hat {\tau }}\cdot {\hat {\tau }}$ vanishes, we have:

${\frac {d({\hat {\tau }}\cdot {\hat {\tau }})}{d\ell }}=0=2{\vec {\eta }}\cdot {\hat {\tau }}$

What makes ${\hat {\eta }}$ and ${\hat {\tau }}$ interesting is that they depend only on the path taken by the particle through space, and not on the rate (speed) at which the particle takes this path. Define the magnitude of ${\vec {\eta }}$ to be $\kappa$, so that:

$\kappa {\hat {\eta }}={\vec {\eta }}$.

Thus, we can take the derivative of velocity, ${\vec {v}}={\hat {\tau }}({\rm {d\ell /dt)}}$, as the derivative of the product of two terms:

${\vec {a}}={\frac {d{\vec {v}}}{dt}}={\frac {d{\hat {\tau }}}{dt}}{\frac {d\ell }{dt}}+{\hat {\tau }}{\frac {d^{2}\ell }{dt^{2}}}=\kappa \left({\frac {d\ell }{dt}}\right)^{2}{\hat {\eta }}+{\frac {d^{2}\ell }{dt^{2}}}{\hat {\tau }}$.

This means first that a particle never accelerates in any direction except the normal or the tangent (or of course a combination of both). That is, it never accelerates at all in the ${\hat {\tau }}\times {\hat {\eta }}$ direction. Furthermore, the acceleration in the tangent direction changes speed and only speed, whereas acceleration in the normal direction changes direction and only direction. To discern the meaning of $\kappa$, we consider a particle making uniform circular motion about a circle of radius R. In x-y space,

${\vec {r}}=[R\cos \omega t,R\sin \omega t]$

It can be shown that $\kappa$ (called the curvature) is given by,

${\vec {r}}=\kappa ={\frac {1}{R}}$

Proving this last step is left as an exercise for the reader/editor.