Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I/Exercise sheet 3

Exercises

Exercise

Determine, for the sets

$M=\{a,b,c,d,e\},\,N=\{a,c,e\},\,P=\{b\},\,R=\{b,d,e,f\},$

the following sets.

1. ${}M\cap N$,
2. ${}M\cap N\cap P\cap R$,
3. ${}M\cup R$,
4. ${}{\left(N\cup P\right)}\cap R$,
5. ${}N\setminus R$,
6. ${}{\left(M\cup P\right)}\setminus {\left(R\setminus N\right)}$,
7. ${}{\left({\left(P\cup R\right)}\cap N\right)}\cap R$,
8. ${}{\left(R\setminus P\right)}\cap {\left(M\setminus N\right)}$.

Exercise

Let ${}LA$ denote the set of capital letters in the Latin alphabet, ${}GA$ the set of capital letters in the Greek alphabet, and ${}RA$ the set of capital letters in the Russian alphabet. Determine the following sets.

1. ${}GA\setminus RA$.
2. ${}{\left(LA\cap GA\right)}\cup {\left(LA\cap RA\right)}$.
3. ${}RA\setminus {\left(GA\cup RA\right)}$.
4. ${}RA\setminus {\left(GA\cup LA\right)}$.
5. ${}{\left(RA\setminus GA\right)}\cap {\left({\left(LA\cup GA\right)}\setminus {\left(GA\cap RA\right)}\right)}$.

Exercise

Let ${}A,\,B$ and ${}C$ denote sets. Prove the identity

${}A\setminus {\left(B\cap C\right)}={\left(A\setminus B\right)}\cup {\left(A\setminus C\right)}\,.$

Exercise

Let ${}A,B$ and ${}C$ denote sets. Prove the following identities.

1. ${}A\cup \emptyset =A\,,$

2. ${}A\cap \emptyset =\emptyset \,,$

3. ${}A\cap B=B\cap A\,,$

4. ${}A\cup B=B\cup A\,,$

5. ${}A\cap (B\cap C)=(A\cap B)\cap C\,,$

6. ${}A\cup (B\cup C)=(A\cup B)\cup C\,,$

7. ${}A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\,,$

8. ${}A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\,,$

9. ${}A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)\,.$

Exercise

Prove the following (set-theoretical versions of) syllogisms of Aristotle. Let ${}A,B,C$ denote sets.

1. Modus Barbara: ${}B\subseteq A$ and ${}C\subseteq B$ imply ${}C\subseteq A$.
2. Modus Celarent: ${}B\cap A=\emptyset$ and ${}C\subseteq B$ imply ${}C\cap A=\emptyset$.
3. Modus Darii: ${}B\subseteq A$ and ${}C\cap B\neq \emptyset$ imply ${}C\cap A\neq \emptyset$.
4. Modus Ferio: ${}B\cap A=\emptyset$ and ${}C\cap B\neq \emptyset$ imply ${}C\not \subseteq A$.
5. Modus Baroco: ${}B\subseteq A$ and ${}B\not \subseteq C$ imply ${}A\not \subseteq C$.

Exercise

Does the "subtraction rule“ hold for the union of sets, i.e., can we infer from ${}A\cup C=B\cup C$ that ${}A=B$ holds?

Exercise

Let ${}A,B,C$ denote sets. Show that the following statements are equivalent.

1. ${}A\subseteq B\cup C$.
2. ${}A\setminus B\subseteq C$
3. ${}A\setminus C\subseteq B$.

Exercise

Sketch the product set ${}\mathbb {N} \times \mathbb {N}$ as a subset of ${}\mathbb {R} \times \mathbb {R}$.

Exercise

Describe for any choice of two of the following geometric sets its product set (including the case where a set is taken twice).

1. A line segment ${}I$.
2. A circle (circumference) ${}K$.
3. A disk ${}D$.
4. A parabola ${}P$.

Which of these product sets can be realized within space, which can't?

Exercise

Sketch the following subsets in ${}\mathbb {R} ^{2}$.

1. ${}{\left\{(x,y)\mid x=7{\text{ or }}y=3\right\}}$,
2. ${}{\left\{(x,y)\mid 7x\geq 3y{\text{ and }}4x\leq y\right\}}$,
3. ${}{\left\{(x,y)\mid x^{2}+y^{2}=0\right\}}$,
4. ${}{\left\{(x,y)\mid x^{2}+y^{2}=1\right\}}$.

Exercise

1. Sketch the set ${}M={\left\{(x,y)\in \mathbb {R} ^{2}\mid 4x-7y=3\right\}}$ and the set ${}N={\left\{(x,y)\in \mathbb {R} ^{2}\mid 3x+2y=5\right\}}$.
2. Determine the intersection ${}M\cap N$ geometrically and computationally.

We recommend illustrating the formulated set identities of the following exercises.

Exercise

Let ${}M$ and ${}N$ denote sets, and let ${}A\subseteq M$ and ${}B\subseteq N$ be subsets. Show the identity

${}{\left(A\times N\right)}\cap {\left(M\times B\right)}=A\times B\,.$

Exercise

Let ${}M$ and ${}N$ denote sets, and let ${}A_{1},A_{2}\subseteq M$ and ${}B_{1},B_{2}\subseteq N$ be subsets. Show the identity

${}{\left(A_{1}\times B_{1}\right)}\cap {\left(A_{2}\times B_{2}\right)}={\left(A_{1}\cap A_{2}\right)}\times {\left(B_{1}\cap B_{2}\right)}\,.$

Exercise

Let ${}P$ be a set of people and ${}V$ the set of the first names and ${}N$ the set of the surnames of these people. Define natural mappings from ${}P$ to ${}V$, to ${}N$ and to ${}V\times N$ and discuss them using the relevant notions for mappings.

Exercise

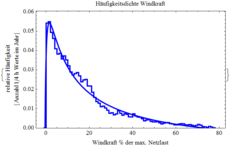
Dr. Peter Klamser

Determine for the following diagrams which empirical mappings they describe. What is in each case the source, the target, which units are used? Does each image represent one or more mappings? Do they really represent mappings? What information is conveyed beyond the mapping? Is there some kind of mathematical modelling for these empirical mappings?

Exercise

Give examples of mappings

$\varphi ,\psi \colon \mathbb {N} \longrightarrow \mathbb {N}$

such that ${}\varphi$ is injective but not surjective, and ${}\psi$ is surjective but not injective.

Exercise

Show that there exists a bijection between ${}\mathbb {N}$ and ${}\mathbb {Z}$.

Exercise

Establish, for each ${}n\in \mathbb {N}$, whether the function

$\mathbb {R} \longrightarrow \mathbb {R} ,x\longmapsto x^{n},$

is injective and/or surjective.

Exercise

Which graphs of a function ${}f\colon \mathbb {R} \rightarrow \mathbb {R}$ do you know from school?

Exercise

How can we recognize by looking at the graph of a mapping

$f\colon \mathbb {R} \longrightarrow \mathbb {R}$

whether ${}f$ is injective or surjective?

Exercise

Which bijective functions ${}f\colon \mathbb {R} \rightarrow \mathbb {R}$ (or between subsets of ${}\mathbb {R}$) do you know from school? What is the name of the inverse function?

Exercise

Let ${}L$ and ${}M$ denote sets. Show that the mapping

$\tau \colon L\times M\longrightarrow M\times L,(x,y)\longmapsto (y,x),$

is a bijective mapping between the product sets ${}L\times M$ and ${}M\times L$.

Exercise

Let ${}L$ and ${}M$ be sets and let

$F\colon L\longrightarrow M$

be a function. Let

$G\colon M\longrightarrow L$

be another function such that ${}F\circ G=\operatorname {Id} _{M}\,$ and ${}G\circ F=\operatorname {Id} _{L}\,$. Show that ${}G$ is the inverse of ${}F$.

Exercise

We consider the sets

$L=\{1,2,3,4,5,6,7,8\},\,M=\{a,b,c,d,e,f,g,h,i\}{\text{ and }}N=\{R,S,T,U,V,W,X,Y,Z\}$

and the mappings ${}\varphi \colon L\rightarrow M$ and ${}\psi \colon M\rightarrow N$ which are given by the value tables

${}x$	${}1$	${}2$	${}3$	${}4$	${}5$	${}6$	${}7$	${}8$
${}\varphi (x)$	${}c$	${}i$	${}a$	${}g$	${}d$	${}e$	${}h$	${}b$

and

${}y$	${}a$	${}b$	${}c$	${}d$	${}e$	${}f$	${}g$	${}h$	${}i$
${}\psi (y)$	${}X$	${}Z$	${}Y$	${}S$	${}Z$	${}S$	${}T$	${}W$	${}U$

respectively.

1. Determine a value table for ${}\psi \circ \varphi$.
2. Are the mappings ${}\varphi$, ${}\psi$, ${}\psi \circ \varphi$ injective?
3. Are the mappings ${}\varphi$, ${}\psi$, ${}\psi \circ \varphi$ surjective?

Exercise

Determine the composite functions ${}\varphi \circ \psi$ and ${}\psi \circ \varphi$ for the functions ${}\varphi ,\psi \colon \mathbb {R} \rightarrow \mathbb {R}$, defined by

$\varphi (x)=x^{4}+3x^{2}-2x+5\,\,{\text{ and }}\,\,\psi (x)=2x^{3}-x^{2}+6x-1.$

Exercise

1. Can a constant mapping be bijective?
2. Is the composition of a constant mapping with an arbitrary mapping (the constant map first) constant?
3. Is the composition of an arbitrary mapping with a constant mapping (the constant map last) constant?

Exercise *

Let ${}L,M,N$ and ${}P$ be sets and let

$F\colon L\longrightarrow M,x\longmapsto F(x),$

$G\colon M\longrightarrow N,y\longmapsto G(y),$

and

$H\colon N\longrightarrow P,z\longmapsto H(z),$

be functions. Show that

${}H\circ (G\circ F)=(H\circ G)\circ F\,.$

Exercise

Let ${}L,\,M$ and ${}N$ denote sets and let

$F\colon L\longrightarrow M,x\longmapsto F(x),$

and

$G\colon M\longrightarrow N,y\longmapsto G(y),$

be mappings with the composition

$G\circ F\colon L\longrightarrow N.$

Show the following properties.

1. If ${}F$ and ${}G$ are injective, then also ${}G\circ F$ is injective.
2. If ${}F$ and ${}G$ are surjective, then also ${}G\circ F$ is surjective.
3. If ${}F$ and ${}G$ are bijective, then also ${}G\circ F$ is bijective.

Exercise *

Let ${}L,M,N$ be sets and let

$f:L\longrightarrow M{\text{ and }}g:M\longrightarrow N$

be mappings with their composition

$g\circ f\colon L\longrightarrow N,x\longmapsto g(f(x)).$

Show that if ${}g\circ f$ is injective, then also ${}f$ is injective.

Hand-in-exercises

Exercise (4 marks)

Let ${}A$ and ${}B$ be sets. Show that the following facts are equivalent.

1. ${}A\subseteq B$,
2. ${}A\cap B=A$
3. ${}A\cup B=B$,
4. ${}A\setminus B=\emptyset$,
5. There exists a set ${}C$ such that ${}B=A\cup C$,
6. There exists a set ${}D$ such that ${}A=B\cap D$.

Exercise (2 marks)

Sketch the following subsets in ${}\mathbb {R} ^{2}$.

1. ${}{\left\{(x,y)\mid 2x=5{\text{ and }}y\geq 3\right\}}$,
2. ${}{\left\{(x,y)\mid -3x\geq 2y{\text{ and }}4x\leq -5y\right\}}$,
3. ${}{\left\{(x,y)\mid y^{2}-y+1\leq 4\right\}}$,
4. ${}{\left\{(x,y)\mid xy=0\right\}}$.

Exercise (3 marks)

Let ${}L,M,N$ be sets, and let

$f:L\longrightarrow M{\text{ and }}g:M\longrightarrow N$

be mappings with their composite mapping

$g\circ f\colon L\longrightarrow N,x\longmapsto g(f(x)).$

Show that if ${}g\circ f$ is surjective, then also ${}g$ is surjective.

Exercise (4 marks)

We consider a computer with only two memory units, each can represent a natural number. At the start of every program (a sequence of commands), the initial entries are ${}(0,0)$. The computer can empty a memory unit, it can increase a memory unit by ${}1$, it can jump to another command (unconditional Goto) and it can compare the two entries of the two memory units. Moreover, it can jump to another command in case the comparing condition is fulfilled (conditional Goto). There is a printing command which prints the entries at the moment. Write a computer-program such that every pair ${}(n,m)\in \mathbb {N} ^{2}$ is printed exactly once.

Exercise (4 marks)

Determine the compositions ${}\varphi \circ \psi$ and ${}\psi \circ \varphi$ for the mappings ${}\varphi ,\psi \colon \mathbb {R} \rightarrow \mathbb {R}$ given by

$\varphi (x)=x^{3}+2x+1\,\,{\text{ and }}\,\,\psi (x)=x^{2}-5.$

Exercise (3 marks)

Consider the set ${}M=\{1,2,3,4,5,6,7,8\}$, and the mapping

$\varphi \colon M\longrightarrow M,x\longmapsto \varphi (x),$

defined by the following table

${}x$	${}1$	${}2$	${}3$	${}4$	${}5$	${}6$	${}7$	${}8$
${}\varphi (x)$	${}2$	${}5$	${}6$	${}1$	${}4$	${}3$	${}7$	${}7$

Compute ${}\varphi ^{1003}$, that is, the ${}1003$-rd composition (or iteration) of ${}\varphi$ with itself.

<< | Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I | >> PDF-version of this exercise sheet Lecture for this exercise sheet (PDF)