Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 45

Relations

Definition

Let ${}X$ and ${}Y$ denote sets. A relation between ${}X$ and ${}Y$ is a subset

${}R\subseteq X\times Y$.

A relation means that certain pairs ${}(x,y)$ belong to the given relation, and the other pairs do not belong to it. We write ${}(x,y)\in R$, or ${}R(x,y)$, or ${}xRy$. In case ${}X=Y$, we talk about a relation on ${}X$. From analysis, order relations are probably known.

Definition

A relation ${}\preccurlyeq$ on a set ${}I$ is called an order relation, if the following three conditions are fulfilled.

1. ${}i\preccurlyeq i$ for all ${}i\in I$.
2. From ${}i\preccurlyeq j$ and ${}j\preccurlyeq k$ we can deduce ${}i\preccurlyeq k$.
3. From ${}i\preccurlyeq j$ and ${}j\preccurlyeq i$ we can deduce ${}i=j$.

These relation properties are called reflexive, transitive, antisymmetric.

Equivalence relations

Definition

An equivalence relation on a set ${}M$ is a relation ${}R\subseteq M\times M$ fulfilling the following three properties (for arbitrary ${}x,y,z\in M$).

1. ${}x\sim x$ (reflexive).
2. ${}x\sim y$ implies ${}y\sim x$ (symmetric).
3. From ${}x\sim y$ and ${}y\sim z$ we can deduce ${}x\sim z$ (transitive).

Here, ${}x\sim y$

means that the pair ${}(x,y)$ belongs to ${}R$.

Example

A basic example of an equivalence relation is the equality on an arbitrary set ${}M$. Under equality, every element is only equivalent with itself.

Wildebeest form an equivalence class with respect to the equivalence relation belonging to the same species, zebras as well.

Example

In many situations, we are not interested in objects individually, instead, we are interested in some of their specific properties. Objects that behave equally with respect to a certain property might be considered as equivalent (with respect to this property). Such an equality with respect to a certain property defines an equivalence relation. If, for example, we are only interested in the color of some objects, then objects that have (exactly) the same color are equivalent to each other. If we are interested, among a collection of animals, not for their individual properties but only for the species they belong to, then two animals are equivalent if and only if they belong to the same species. Students might be considered as equivalent if they study the same combination of subjects. Vectors can be considered as equivalent if they have the same distance to the origin, etc. An equivalence relation is typically a certain way to look at certain objects, which considers certain objects as equal.

In such examples from "daily life“, one has to be cautious, as these properties are usually not defined as precisely as mathematical concepts. In everyday life, similarity is more important that equality with respect to a certain property. However, similarity is not an equivalence relation; it is reflexive and symmetric but not transitive. If ${}A$ and ${}B$ are similar, and ${}B$ and ${}C$ as well, then ${}A$ and ${}C$ might be already not similar any more (in the same way: is a neighbor of, is related to, etc.).

The equality with respect to a property can be made precise by the following mathematical construction.

Example

Let ${}M$ and ${}N$ be sets, and let ${}f\colon M\rightarrow N$ denote a mapping. In such a situation, we always get an equivalence relation on the domain ${}M$ of the mapping by declaring two elements ${}x,y\in M$ to be equivalent if they map under ${}f$ to the same element, that is, if ${}f(x)=f(y)$ holds. If the mapping ${}f$ is injective, then the equivalence relation defined by ${}f$ on ${}M$ is the equality. If the mapping is constant, then all elements from ${}M$ are equivalent under the corresponding equivalence relation.

For a mapping ${}f\colon M\rightarrow N$, the set of all points ${}x\in M$ mapping to a certain point ${}z\in N$ is called the fiber over ${}z$. In this situation ,the equivalence classes (see below) are just the fibers.

Example

Let ${}d\in \mathbb {N}$ be fixed. We consider on ${}\mathbb {Z}$ the equivalence relation ${}\sim$, where two numbers ${}a,b\in \mathbb {Z}$ are considered to be equivalent if their difference ${}a-b$ is a multiple of ${}d$. Two numbers are equivalent if and only if it is possible to reach from one number the other number by jumps of length ${}d$. Using division with remainder, this means that two numbers are equivalent to each other if, upon division by ${}d$, they leave the same remainder.

Example

We consider the floor of a real number, that is, the mapping

$\lfloor \,\,\rfloor \colon \mathbb {R} \longrightarrow \mathbb {Z} ,t\longmapsto \lfloor t\rfloor .$

A real number ${}t$ is mapped to the largest integer number that is smaller or equal ${}t$. Here, the interval ${}[n,n+1)$ (with integer bound ${}n$, closed on the left, open on the right) is mapped to ${}n\in \mathbb {Z}$. With respect to this mapping, two real numbers are equivalent if and only if they lie in the same interval of this type. In the decimal expansion, this means that their digits before the point are identical.

We can also consider the digits after the point. This corresponds to the mapping

$\mathbb {R} \longrightarrow [0,1),t\longmapsto t-\lfloor t\rfloor .$

Under the equivalence relation defined by this mapping, two real numbers are equivalent if their digits after the point are identical. This is the case if and only if their difference is an integer number.

Equivalence classes and system of representatives

An equivalence relation ${}R\subseteq M\times M$ on a set ${}M$ may also be considered as a partition of the set ${}M$. In order to see this, the concept of an equivalence class is helpful.

Definition

Let ${}R\subseteq M\times M$ be an equivalence relation, and let ${}x\in M$. Then

${}[x]:={\left\{y\in M\mid (x,y)\in R\right\}}\,$

is called the equivalence class of ${}x$ with respect to ${}R$.

Hence, ${}[x]$ is the subset of all elements of ${}M$ that are equivalent with ${}x$. Every element ${}y\in [x]$ is called a representative of the equivalence class ${}[x]$.

Definition

Let ${}\sim$ be an equivalence relation on a set ${}M$. A subset ${}T\subseteq M$ is called a system of representatives for the equivalence relation, if for every equivalence class

there exists exactly one element in ${}T$ of this class.

Three equivalence classes for the equivalence relation given by being parallel.

Example

On the set of all lines in the plane, we can consider the property of being parallel as an equivalence relation. A line is parallel to itself, the relation is obviously symmetric, and if ${}G_{1}$ and ${}G_{2}$ are parallel, and ${}G_{2}$ and ${}G_{3}$ are parallel, then also ${}G_{1}$ and ${}G_{3}$ are parallel. The equivalence class of a line ${}G$ consists of all lines that are parallel to ${}G$; these lines form a parallel linenschar. We fix a point ${}M$ in the plane. Then there exists, for every line ${}G$, a parallel line ${}G'$ running through ${}M$. Therefore, every equivalence class can be uniquely represented by a line through the point ${}M$. The set of lines through ${}M$ form a system of representatives for this equivalence relation.

Under the equivalence relation "accessible overland“, the islands and the continents are the equivalence classes.

Example

Suppose that we are in a situation, where certain places (or Objects) can be reached from certain other places or not. This accessibility can be determined by the choice of means of transport, or by a more abstract kind of movement. Such an accessibility relation yields often an equivalence relation. A place can be reached by starting at this place, this gives reflexivity. The symmetry of accessibility means that if it is possible to reach ${}A$ starting from ${}B$, then it is also possible to reach ${}B$ starting from ${}A$. This is a natural condition for accessibility, though it is probably not fulfilled for every kind of accessibility. The transitivity does hold whenever we can do the movements after each other, like going from ${}A$ to ${}B$, and then from ${}B$ to ${}C$.

If, for example, accessible is given by walking overland, then two places are equivalent if and only if they lie on the same island (or continent). Islands and continents are the equivalence classes. In topology, the concept of path-connectedness plays an important role: two points are path-connected if they can be connected by a continuous path. Or: On the set of integer number, there is a colony of fleas, and every jump of a flea has the length of five unites (in both directions). How many flea populations are there, which fleas can meet each other?

Example

In chess, a bishop can move diagonally and arbitrarily far in every direction. Two squares (positions) on a chess board are called bishop-equivalent if it is possible to reach, starting from one square, by finitely many bishop moves, the other square. This is an equivalence relation on the chess board. Moving diagonally, the color of the position does not change; therefore, a bishop standing on a white square will always stay on a white square. Moreover, a bishop, standing on a white square, can reach every white square. Hence, there are only two equivalence classes: the white squares and the black squares; accordingly, we talk about the light-squared and the dark-squared bishop (this is not the color of the piece).

Example

Visualization of the example. The equivalence classes are colored differently.

We consider the lattice product set ${}M=\mathbb {N} \times \mathbb {N}$. We fix the jumps (think about a Meadow jumping mouse that can perform these jumps and no other jumps)

$\pm (2,0)\,\,{\text{ and }}\,\,\pm (3,3).$

We say that two points ${}P=(a,b),\,Q=(c,d)\in M$ are equivalent if it is possible, starting in ${}P$, to reach the point ${}Q$ with a sequence of such jumps. This defines an equivalence relation (the main reason is that for every jump also its negative jump is allowed). Typical questions are: How can we characterize equivalent points, how can we decide whether two points are equivalent or not?

Quotient set and canonical mapping

Definition

Let ${}R\subseteq M\times M$ denote an equivalence relation. The set

${}M/R:={\left\{[x]\mid x\in M\right\}}\,$

is called the quotient set of ${}R$.

Definition

Let ${}R\subseteq M\times M$ denote an equivalence relation, and let ${}M/R$ be the quotient set. The mapping

$q_{R}\colon M\longrightarrow M/R,x\longmapsto [x],$

is called the canonical projection of ${}R$.

With the quotient set, the equivalence classes become elements of a new set. Under the canonical projection, equivalent elements are mapped to the same element and so they are identified. We also say that the theory of equivalence relations is the art of identifying. In working with quotient sets, the proper definition is not so important any more; instead, we work rather with the intrinsic properties of these sets. The following statement says, in particular, that every equivalence relation can be obtained as in example *****. Therefore, equivalent always means equal under a suitable mapping.

Lemma

Let ${}M$ be a set, and let ${}\sim$ denote an equivalence relation on ${}M$, together with the equivalence classes ${}[x]$ and the quotienten set

${}M/\sim$. Then the following statements hold.

1. ${}x\sim y$ if and only if ${}[x]=[y]$, and this holds if and only if ${}[x]\cap [y]\neq \emptyset$.
2. ${}M=\bigcup _{[x]\in M/\sim }[x]$ is a disjoint union.
3. The canonical projection

   $q\colon M\longrightarrow M/\sim ,x\longmapsto [x],$

   is surjective.

4. We have ${}q^{-1}([x])=[x]$.

Proof

1. Let ${}x$ and ${}y$ be equivalent, and ${}u\in [x]$. Then ${}x\sim u$, and, by transitivity, also ${}y\sim u$, thus ${}u\in [y]$. Therefore, the equivalence classes coincide. The implication from the middle to the right is clear, because, due to ${}x\sim x$, the equivalence classes are not empty. Suppose now that ${}[x]\cap [y]\neq \emptyset$, and let ${}z$ denote an element in the intersection. Then ${}x\sim z$ and ${}y\sim z$, and, by transitivity, ${}x\sim y$.
2. Because of the reflexivity, we have ${}x\in [x]$; therefore, ${}M=\bigcup _{[x]\in M/\sim }[x]$. This union is disjoint by part (1).
3. The surjectivity is clear because of the definition of the quotient set, and since ${}x$ is sent to the class ${}[x]$.
4. We have

   ${}q^{-1}([x])={\left\{y\in M\mid q(y)=[x]\right\}}={\left\{y\in M\mid [y]=[x]\right\}}={\left\{y\in M\mid y\sim x\right\}}=[x]\,.$

$\Box$

Important mathematical constructions can be described as a quotient set to a certain equivalence relation on a simpler set. This is illustrated by the following examples.

Example

Let ${}n\in \mathbb {N}$, and set ${}M=\mathbb {R} ^{n+1}\setminus \{0\}$. ${}\mathbb {R} ^{n+1}$ is a real vector space, the scalar multiplication of ${}\lambda \in \mathbb {R}$ and ${}x\in \mathbb {R} ^{n+1}$ is denoted by ${}\lambda \cdot x$ Moreover, set

$R={\left\{(x,y)\in M\times M\mid {\text{ there exists some }}\lambda \in \mathbb {R} \setminus \{0\}{\text{ such that }}\lambda \cdot x=y\right\}}\,.$

Therefore, two points are defined to be equivalent if they can be transformed to each other by scalar multiplication with a scalar ${}\lambda \neq 0$. We can also say that two points are equivalent if they define the same line through the origin.

This is indeed an equivalence relation. The reflexivity follows from ${}x=1x$ for every ${}x\in M$. To prove symmetry, suppose ${}xRy$, that is, there exists some ${}\lambda \neq 0$ such that ${}\lambda x=y$. Then also ${}y=\lambda ^{-1}x$ holds, as ${}\lambda$ has an inverse element. To prove transitivity, suppose that ${}xRy$ and ${}yRz$ holds; this means that there exist ${}\lambda ,\delta \neq 0$ such that ${}\lambda x=y$ and ${}\delta y=z$. Then ${}z=\delta y=(\delta \lambda )x$ with ${}\delta \lambda \neq 0$. The equivalence classes of this equivalence relation are the lines through the origin (but without the origin). The quotient set is called the real-projective space (of real dimension ${}n$), and is denoted by ${}{\mathbb {P} }_{\mathbb {R} }^{n}$.

Example

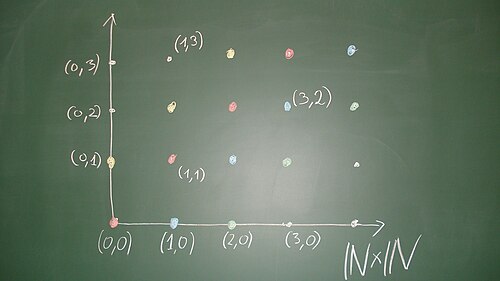
Let ${}\mathbb {N}$ be the set of the natural numbers, and let ${}M=\mathbb {N} \times \mathbb {N}$ denote the product set with the componentwise addition. We define on ${}M$ a relation by

$(a,b)\sim (c,d),{\text{ if }}a+d=b+c.$

This holds, in case ${}a\leq c$, if and only if there exists an ${}e\in \mathbb {N}$ (namely ${}e=c-a$) such that

${}(c,d)=(a,b)+(e,e)\,.$

This means that the pairs differ by an diagonal element, that is, a pair, where both components coincide. This relation is an equivalence relation on ${}M$, see exercise *****. If we consider ${}\mathbb {N} \times \mathbb {N}$ as a square lattice (a "discrete coordinate system“), then the equivalence classes are given by the points on a "discrete line“ parallel to the diagonal. The points ${}(a,b)$ with ${}a\geq b$ are equivalent with ${}(a-b,0)$; they have a representative where the second component is ${}0$. The points ${}(a,b)$ with ${}a\leq b$ are equivalent to ${}(0,b-a)$; they have a representative where the first component is ${}0$. The points ${}(a,a)$ are equivalent to ${}(0,0)$. We call the representative of an equivalence class where at least one component is ${}0$, the standard representative of this equivalence class. The standard representatives are the discrete points of the confining lines of the quadrant; for a point, we find its standard representative by going, parallel to the diagonal, in direction of these lines. Two points are equivalent if and only if they have the same standard representative.

We call now the quotient set, that is, the set of the equivalence classes under this equivalence relation, the set of the integer numbers, and denote it with ${}\mathbb {Z}$. Every integer number has exactly one standard representative of the form ${}n:=(n,0)$ with ${}n\in \mathbb {N} _{+}$, or of the form ${}0:=(0,0)$, or of the form ${}-n:=(0,n)$ with ${}n\in \mathbb {N} _{+}$. We consider a natural number ${}n$ as the integer number ${}(n,0)$.

We want to "add“ two integer numbers, that is, two such equivalence classes ${}[(a,b)]$ and ${}[(c,d)]$, in order to get a binary operation ${}\oplus$ on ${}\mathbb {Z}$. The first idea that comes to mind is to define this via

${}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,.$

However, here we encounter the problem whether this is well-defined, since this operation is defined using certain representatives; it is not clear at all whether different representatives give the same result. Therefore, if ${}(a,b)\sim (a',b')$ and ${}(c,d)\sim (c',d')$ holds, then we have to check that also

${}(a+c,b+d)\sim (a'+c',b'+d')\,$

holds, which means ${}[(a+c,b+d)]=[(a'+c',b'+d')]$. This is the case, see exercise *****. Moreover, one can show that this operation on ${}\mathbb {Z}$ is associative and commutative, that ${}[(0,0)]$ is the neutral element of this operation, and that for every element ${}[(a,b)]$ there exists an inverse element, namely ${}[(b,a)]$.

We define now a multiplication on ${}\mathbb {Z}$ via

${}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.$

Again, this is well-defined, and one can show that the multiplication is associative and commutative, that ${}1=[(1,0)]$ is the neutral element, and that the distributive law holds.

The following proposition describes the universal property of the quotient set.

Lemma

Let ${}M$ be a set, and let ${}\sim$ denote an equivalence relation on ${}M$, with the quotient set ${}M/\sim$. Let ${}\varphi \colon M\rightarrow W$ be a mapping with ${}\varphi (x)=\varphi (y)$ for all ${}x,y\in M$ with ${}x\sim y$. Then there exists a uniquely determined mapping ${}{\overline {\varphi }}\colon M/\sim \,\,\rightarrow W$ fulfilling

${}\varphi ={\overline {\varphi }}\circ q$.

Proof

Let ${}[x]\in M/\sim$ be given. The only possibility for ${}{\overline {\varphi }}$ is to set ${}{\overline {\varphi }}([x]):=\varphi (x)$. We have to show that this mapping is well-defined, that is, independent of the choice of the representatives. For this, let ${}[x]=[y]$, that is, ${}x\sim y$. By the condition on ${}\varphi$, we have ${}\varphi (x)=\varphi (y)$.

$\Box$

Footnotes