Complex Numbers
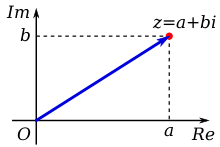
In mathematics, a complex number is an element of a number system that contains the real numbers and a specific element denoted , called the imaginary unit, satisfying . Moreover, every complex number can be expressed in the form , where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number , is called the real part and is called the imaginary part. The set of complex numbers is typically denoted by the symbol . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.[1]