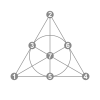
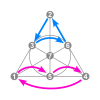
3-bit Walsh permutation/cycle shapes

This table shows the 24 arrow patterns of the 168 3-bit Walsh permutations (as Fano plane collineations).

matrix sums from 3 to 6	fixed points
2 2 (Europe) 2 4 (America) 3 3 (Asia) 7 (Africa) the four non-trivial cycle types

The typical shape of a collection is a hexagon, showing the two rotations and three reflections of some initial pattern.
The one pattern with rotational symmetry is shown as a pair. Patterns with mirror symmetry are shown as triangles.
Where the hexagon or triangle does not contain the inverse permutations, two nested polygons are shown.
These are the types of collections shown below:

• neutral permutation
• 1 pair (of rotations)


• 5 single triangles
• 1 double triangle


• 8 single hexagons
• 8 double hexagons

In the column graph, the shown permutations are highlighted in the respective component of the neighbor graph. All except 9 are in the cube-like clusters with 25 vertices. Apart from the center, there are four types of vertices, which are marked with suits.

Each permutation has a set of fixed points.

• The neutral permutation has only fixed points.
• 7-cycles have none.


• For cycle type 2+2 they form a line of the Fano plane.


• Cycle types 2+4 and 3+3 have single fixed points.

The points can be characterized by their binary weight, and the lines by the weights of their points. This property is in the column fixed.

size	collection	graph	det	sum	cycles	fixed
&1 1	124		&1 +	3	&0	&1 ⊤
&5 6	134 164 324 126 524 125	Paris	&1 +	4	&2 22	&2 121
&3 3	127 724 174	Rometranspose of Florence	&1 +	5a	&2 22	&2 121
&3 3	564 135 326	Florencetranspose of Rome	&1 +	5a	&2 22	&3 132
&6 6 * 2	175 574 165 534 726 327 526 325 364 136 764 137	Buenos Aires inside: 5 outside: 6	&1 +	5b 6	&3 24	&5 1
&2 2	241 412	Tokyo	&1 +	3	&4 33	&7 3
&5 6	741 417 472 271 247 712	New Yorktranspose of San Francisco	&1 +	5a	&3 24	&6 2
&5 6	513 645 263 632 456 351	San Franciscotranspose of New York	&1 +	5a	&3 24	&7 3
&6 6 * 2	612 243 245 512 251 452 416 341 261 432 413 641	Cairo inside: a outside: b	&1 +	4	&5 7	&8 ⊥
&6 6 * 2	732 267 643 613 371 476 453 651 253 652 517 745	Baghdadcompare Alexandria inside: 5 outside: 6	&1 +	5b 6	&4 33	&6 2
&6 6 * 2	457 751 361 436 647 713 532 265 345 516 672 273	Alexandriacompare Baghdad inside: b (5b) outside: a (6)	&1 +	5b 6	&5 7	&8 ⊥
&6 6 * 2	763 637 375 576 573 675 736 367 765 537 357 756	Tripoli inside: a (+) outside: b (−)	&2 ±	7	&5 7	&8 ⊥
&4 3 * 2	567 735 657 753 673 376	Santiago inside: + outside: −	&2 ±	7	&3 24	&6 2
&3 3	214 142 421	London	&3 −	3	&2 22	&3 132
&3 3	217 742 471	Berlintranspose of Hamburg	&3 −	5a	&2 22	&4 222
&3 3	654 153 623	Hamburgtranspose of Berlin	&3 −	5a	&2 22	&3 132
&5 6	274 172 714 147 721 427	Beijingtranspose of Shanghai	&3 −	5a	&4 33	&5 1
&5 6	236 362 315 546 531 465	Shanghaitranspose of Beijing	&3 −	5a	&4 33	&7 3
&5 6	234 162 314 146 521 425	Seoul	&3 −	4	&4 33	&5 1
&5 6	216 342 215 542 431 461	Torontotranspose of Montreal	&3 −	4	&3 24	&6 2
&5 6	254 152 614 143 621 423	Montrealtranspose of Toronto	&3 −	4	&3 24	&5 1
&6 6 * 2	237 762 316 346 317 746 235 562 435 561 571 475	Delhitranspose of Mumbai inside: 5 outside: 6	&3 −	5b 6	&4 33	&6 2
&6 6 * 2	674 173 354 156 754 157 634 163 625 523 723 627	Mumbaitranspose of Delhi inside: 5 outside: 6	&3 −	5b 6	&4 33	&5 1
&6 6 * 2	276 372 615 543 715 547 256 352 463 631 731 467	Cape Town inside: a (5b) outside: b (6)	&3 −	5b 6	&5 7	&8 ⊥